Introduction
In the world of mathematics, the recent discovery of the ninth Dedekind number has sparked a wave of excitement. This monumental find, the result of over three decades of research, marks a significant milestone in the field. Join us as we delve into the intriguing realm of Dedekind numbers, exploring their history, the journey to this latest discovery, and the profound impact they have on our understanding of mathematics.
- Introduction
- The Discovery of the Ninth Dedekind Number
- What are Dedekind Numbers?
- The History of Dedekind Numbers
- The Significance of the Discovery
- The Future of Dedekind Numbers
- Conclusion
The Discovery of the Ninth Dedekind Number
The quest for the ninth Dedekind number was a formidable challenge that spanned over 32 years. The calculations involved were so complex and involved such large numbers that it was uncertain whether D(9) would ever be discovered. But undeterred by the complexity and the enormity of the task, mathematicians continued their pursuit.
The breakthrough came with the help of a special kind of supercomputer that uses specialized units called Field Programmable Gate Arrays (FPGAs). These units can perform multiple calculations in parallel, making them ideal for tackling the enormous calculations required to discover D(9). The supercomputer, named Noctua 2, is housed at the University of Paderborn in Germany.
After five months of relentless computing, Noctua 2 finally came up with an answer, and the ninth Dedekind number, a 42-digit monster, was discovered. The number is calculated to be 286 386 577 668 298 411 128 469 151 667 598 498 812 366.
What are Dedekind Numbers?
Dedekind numbers, denoted as M(n), represent the count of different monotonic Boolean functions on n variables. A monotonic Boolean function is one where changing an input from false to true can only cause the output to change from false to true and not the other way around. These numbers have connections to antichains of sets, lattice theory, and abstract simplicial complexes.
An antichain is a collection of sets, none of which is a subset of another set. By associating an antichain of subsets of Boolean variables with a monotonic Boolean function, we can define a function that returns true if any subset of true inputs belongs to the antichain. Similarly, every monotonic Boolean function can be linked to an antichain of minimal subsets of variables that force the function to be true.
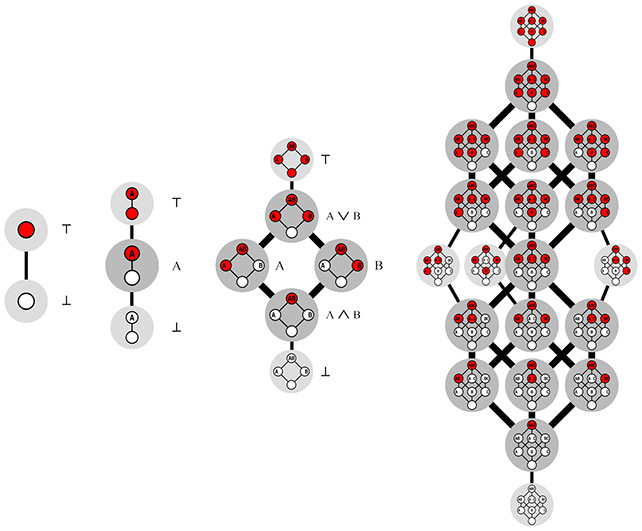
In lattice theory, the family of all monotonic Boolean functions, together with logical conjunction (AND) and disjunction (OR), forms a distributive lattice. This lattice is constructed from the partially ordered set of subsets of the variables.
Dedekind numbers also correspond to the count of abstract simplicial complexes on n elements. These complexes are families of sets where any subset of a set in the family is also in the family. An antichain can define a simplicial complex, and the maximal simplices in a complex form an antichain.
The values of the Dedekind numbers for n = 0 to 9 are 2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788, and 286386577668298411128469151667598498812366.
The History of Dedekind Numbers
The journey of Dedekind numbers began with Richard Dedekind, a German mathematician who made significant contributions to abstract algebra, number theory, and the foundations of mathematics. However, the concept of Dedekind numbers, as we understand it today, has evolved over time and is a result of the collective efforts of many mathematicians.
The first few Dedekind numbers are relatively straightforward. Mathematicians count D(1) as just 2, then 3, 6, 20, 168, and so on. However, as the numbers increase, the complexity of calculating them also escalates.
In 1991, a significant milestone was achieved when the eighth Dedekind number, D(8), was discovered. This 23-digit number was calculated using a Cray-2 supercomputer, one of the most powerful supercomputers of the time, and it took mathematician Doug Wiedemann 200 hours to figure it out. This discovery set the stage for the search for the next Dedekind number, D(9).
The Significance of the Discovery
The discovery of the ninth Dedekind number is a monumental achievement in the field of mathematics. It represents the culmination of over three decades of persistent research and the successful application of advanced computational technology.
The Dedekind numbers, though abstract and complex, have profound implications in various areas of mathematics and computer science. They are closely related to monotone Boolean functions, which are fundamental in digital circuit design, machine learning, and data mining. The discovery of D(9) not only expands our understanding of these functions but also opens up new possibilities for their application.
Moreover, the discovery showcases the power of modern supercomputers and their potential to solve complex mathematical problems. The use of Field Programmable Gate Arrays (FPGAs) in the Noctua 2 supercomputer demonstrates how parallel computing can be leveraged to tackle enormous calculations, setting a precedent for future mathematical explorations.
The Future of Dedekind Numbers
The journey of Dedekind numbers is far from over. With the discovery of D(9), the stage is set for the search for the next Dedekind number, D(10). Given the complexity and the computational power required to calculate D(9), it’s conceivable that the discovery of D(10) may be years, if not decades, away.
However, the quest for D(10) and beyond is more than just a mathematical challenge. It represents the human spirit of curiosity, the desire to push the boundaries of knowledge, and the relentless pursuit of understanding the complex language of the universe – mathematics.
In the meantime, researchers will continue to explore the applications of Dedekind numbers and monotone Boolean functions in various fields. As we venture further into the era of big data and artificial intelligence, the role of these mathematical concepts is likely to become even more significant.
Conclusion
The discovery of the ninth Dedekind number is a testament to the power of persistence, the potential of technology, and the beauty of mathematics. It’s a story of a three-decade-long journey that culminated in the unveiling of a 42-digit mathematical marvel, a journey that was made possible by the relentless pursuit of knowledge by mathematicians and the incredible computational capabilities of modern supercomputers.
Dedekind numbers, though abstract and complex, are a crucial part of the mathematical landscape. They are intertwined with monotone Boolean functions, which have significant applications in computer science and digital technology. The discovery of D(9) not only expands our understanding of these numbers but also opens up new avenues for their application.
As we look to the future, the quest for the next Dedekind number, D(10), looms on the horizon. It’s a challenge that will undoubtedly push the boundaries of mathematical research and computational capabilities. But if the discovery of D(9) has taught us anything, it’s that no mathematical challenge is insurmountable.
In the end, the journey of Dedekind numbers is a reflection of our own journey as seekers of knowledge. It’s a journey marked by curiosity, persistence, and the relentless pursuit of understanding the universe’s complex language – mathematics.
And so, as we celebrate the discovery of the ninth Dedekind number, we also look forward to the mathematical marvels that await us in the future. Because in the world of mathematics, every discovery is just the beginning of a new journey.
That concludes our exploration of Dedekind numbers and the remarkable discovery of the ninth Dedekind number. The world of mathematics is vast and full of wonders, and we’ve only just scratched the surface. So, keep exploring, keep learning, and keep marveling at the beauty of mathematics.