Home Blog

5 Powerful Uses of the Agentic AI Browser, Comet by Perplexity

Shounak Das
-
0

In the ever-evolving landscape of the internet, we’ve grown accustomed to a certain way of doing things. We open a browser, type in a query, and are presented with a list of links. We then open multiple tabs, sift through information, and piece together the answers we need. While this process has served us for decades, it’s often cumbersome, time-consuming, and frankly, a bit chaotic. But what if your browser could do the heavy lifting for you? What if it could understand your intentions, perform complex tasks, and act as a true assistant?

Enter the age of the agentic browser, a revolutionary technology that is set to redefine our relationship with the internet. And at the forefront of this transformation is Comet, the groundbreaking new browser from the AI pioneers at Perplexity. Comet isn’t just a new interface for the web; it’s a paradigm shift. It’s a browser that doesn’t just display information but actively works on your behalf.

So, what exactly is an agentic browser? Imagine a browser with a built-in AI that can understand natural language commands, navigate websites, fill out forms, compare products, and even make purchases for you. It’s a browser that transforms from a passive tool into a proactive partner.

Exclusive Invite

In this blog post, we’ll explore five powerful use cases of Perplexity’s Comet that showcase how this agentic browser is set to revolutionize your online experience.

1. Supercharge Your Research and Learning

Whether you’re a student writing a research paper, a professional staying on top of industry trends, or simply a curious mind exploring a new topic, the internet is your greatest resource. However, it can also be an overwhelming sea of information. Comet’s agentic capabilities turn this information overload into a streamlined and efficient learning experience.

From Information Overload to Instant Insights

With Comet, you can say goodbye to the tedious process of opening countless tabs and reading through lengthy articles. Its built-in AI assistant can instantly summarize web pages, PDF documents, and even videos, providing you with the key takeaways in a matter of seconds. Imagine you’re faced with a 50-page academic paper. Instead of spending an hour reading it, you can simply ask Comet, “Summarize the key findings of this paper.”

But it doesn’t stop there. Comet’s contextual awareness allows it to understand the content you’re viewing and answer your questions in a conversational manner. If you come across a complex concept, you can highlight the text and ask Comet, “Explain this to me like I’m a beginner.” This feature is a game-changer for anyone looking to grasp difficult subjects without getting lost in jargon.

In Practice:

  • For Students: Quickly summarize lecture notes, research papers, and online articles for your assignments.
  • For Professionals: Stay informed about the latest industry news and reports by summarizing articles and white papers.
  • For Lifelong Learners: Explore new topics with ease by getting concise summaries and clear explanations of complex ideas.

2. Seamless and Intelligent Shopping

Online shopping is convenient, but it can also be a chore. Comparing products, hunting for the best deals, and navigating through checkout processes can be a time-consuming and frustrating experience. Comet transforms your browser into a personal shopping assistant, making the entire process faster, easier, and more intelligent.

Your Personal Shopping Guru

With Comet, you can simply tell your browser what you’re looking for, and it will do the rest. For instance, you could say, “Find me the best-rated noise-canceling headphones under 300." Comet will then browse multiple e-commerce sites, compare prices, read reviews, and present you with a curated list of options. <!-- /wp:paragraph --> <!-- wp:paragraph --> But the real magic happens when you've made your decision. Comet can then proceed to checkout, fill in your shipping and payment information (securely, of course), and complete the purchase for you. This level of automation is unprecedented and turns the often-tedious process of online shopping into a truly seamless experience. <!-- /wp:paragraph --> <!-- wp:paragraph --> <strong>In Practice:</strong> <!-- /wp:paragraph --> <!-- wp:list --> <ul class="wp-block-list"><!-- wp:list-item --> <li><strong>Comparison Shopping:</strong> Effortlessly compare prices and features of products across different retailers.</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li><strong>Finding the Best Deals:</strong> Let Comet hunt for discounts, coupons, and special offers for you.</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li><strong>Effortless Checkout:</strong> Breeze through the checkout process with Comet's automated form-filling capabilities.</li> <!-- /wp:list-item --></ul> <!-- /wp:list --> <!-- wp:heading --> <h2 class="wp-block-heading">3. Automated Task Management and Productivity</h2> <!-- /wp:heading --> <!-- wp:paragraph --> In today's fast-paced world, we're all juggling multiple tasks and responsibilities. Comet's agentic AI is designed to be your personal productivity powerhouse, helping you manage your daily workflow with ease and efficiency. From scheduling meetings to organizing your digital workspace, Comet has you covered. <!-- /wp:paragraph --> <!-- wp:heading {"level":3} --> <h3 class="wp-block-heading">The Ultimate Productivity Partner</h3> <!-- /wp:heading --> <!-- wp:paragraph --> One of Comet's standout features is its ability to interact with your other online tools. For example, you can connect your Google Calendar and Gmail accounts and then simply ask Comet to "schedule a meeting with John for next Tuesday afternoon." Comet will then find a time that works for both of you and send out the invitation. <!-- /wp:paragraph --> <!-- wp:paragraph --> Comet also helps you stay organized with its "Workspaces" feature. Instead of having a cluttered mess of tabs, you can group related tabs into dedicated workspaces. This is incredibly useful for managing multiple projects or research topics. And when you're done, you can simply close the entire workspace, knowing that you can easily revisit it later. <!-- /wp:paragraph --> <!-- wp:paragraph --> <strong>In Practice:</strong> <!-- /wp:paragraph --> <!-- wp:list --> <ul class="wp-block-list"><!-- wp:list-item --> <li><strong>Effortless Scheduling:</strong> Schedule meetings, appointments, and events with a simple voice or text command.</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li><strong>Organized Browsing:</strong> Keep your tabs organized and your mind focused with Comet's Workspaces.</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li><strong>Email Management:</strong> Let Comet help you draft emails, find important messages, and manage your inbox.</li> <!-- /wp:list-item --></ul> <!-- /wp:list --> <!-- wp:heading --> <h2 class="wp-block-heading">4. Streamlined Travel Planning</h2> <!-- /wp:heading --> <!-- wp:paragraph --> Planning a trip can be an exciting prospect, but the logistics can quickly become overwhelming. From finding the best flights and accommodations to creating an itinerary, there are a lot of moving parts. Comet's agentic capabilities make travel planning a breeze, turning what was once a stressful process into an enjoyable experience. <!-- /wp:paragraph --> <!-- wp:heading {"level":3} --> <h3 class="wp-block-heading">Your AI-Powered Travel Agent</h3> <!-- /wp:heading --> <!-- wp:paragraph --> Imagine you're planning a vacation to Hawaii. Instead of spending hours on different travel websites, you can simply tell Comet, "Find me a round-trip flight to Honolulu from San Francisco for the first week of December, and a beachfront hotel for under400 a night.” Comet will then scour the web, compare options, and present you with a personalized itinerary.

Once you’ve made your choices, Comet can proceed to book your flights and hotel, just like a human travel agent. This end-to-end automation is a game-changer for anyone who loves to travel but dreads the planning process.

In Practice:

  • Finding the Best Flights and Hotels: Let Comet find the best deals on flights and accommodations based on your preferences.
  • Creating an Itinerary: Get help planning your daily activities, finding restaurants, and discovering local attractions.
  • Effortless Booking: Book your entire trip with a few simple commands, without ever having to leave your browser.

5. Empowering Developers and Tech Professionals

For developers, programmers, and other tech professionals, the browser is an indispensable tool. From looking up documentation to debugging code, a significant portion of their workday is spent online. Comet offers a range of features that are specifically designed to streamline these technical tasks and boost productivity.

Exclusive Invite

A Developer’s Best Friend

Comet’s AI assistant can understand and even write code. If you’re stuck on a particular problem, you can ask Comet to “write a Python script that scrapes data from this website.” It can also help you debug your code by identifying errors and suggesting solutions.

Furthermore, Comet can interact with popular developer platforms like GitHub and LeetCode. You can ask it to find a specific library, compare different coding solutions, or even generate documentation for your projects. This level of integration makes Comet an invaluable tool for anyone working in the tech industry.

In Practice:

  • Code Generation and Debugging: Get help writing and debugging code with Comet’s AI-powered assistance.
  • Technical Research: Quickly find the information you need from documentation, forums, and other technical resources.
  • Platform Integration: Interact with your favorite developer platforms directly from your browser.

The Future is Agentic

Perplexity’s Comet is more than just a new browser; it’s a glimpse into the future of how we will interact with the internet. By transforming the browser from a passive tool into an active, intelligent assistant, Comet is paving the way for a more intuitive, efficient, and personalized online experience.

The five use cases we’ve explored here are just the beginning. As agentic AI technology continues to evolve, we can expect to see even more innovative and powerful applications emerge. The future of browsing is here, and it’s agentic. Are you ready to take the leap?

How I Earned $146 in One Month with Beer Money Opportunities

Shounak Das
-
0
How I Earned $146 in One Month with Beer Money Opportunities

Earning extra income online is no longer a myth—it’s a reality, especially with the rise of beer money opportunities. These aren’t full-time jobs but casual, low-effort gigs that can bring in supplementary income while you relax, study, or wait for your food to cook. If you’re based in India like me, it’s even more exciting because several platforms have opened their doors to international users, including Indian participants. In this blog, I’ll share how I earned 146 this month</strong> by leveraging legit beer money sites and testing platforms. <!-- /wp:paragraph --> <!-- wp:paragraph --> Let's dive in. <!-- /wp:paragraph --> <!-- wp:paragraph {"dropCapStyle":"dropcapp"} --> Summary Table: <!-- /wp:paragraph --> <!-- wp:html --> <style type="text/css">@import url("https://assets.mlcdn.com/fonts.css?version=1750852");</style> <style type="text/css"> /* LOADER */ .ml-form-embedSubmitLoad { display: inline-block; width: 20px; height: 20px; } .g-recaptcha { transform: scale(1); -webkit-transform: scale(1); transform-origin: 0 0; -webkit-transform-origin: 0 0; height: ; } .sr-only { position: absolute; width: 1px; height: 1px; padding: 0; margin: -1px; overflow: hidden; clip: rect(0,0,0,0); border: 0; } .ml-form-embedSubmitLoad:after { content: " "; display: block; width: 11px; height: 11px; margin: 1px; border-radius: 50%; border: 4px solid #fff; border-color: #ffffff #ffffff #ffffff transparent; animation: ml-form-embedSubmitLoad 1.2s linear infinite; } @keyframes ml-form-embedSubmitLoad { 0% { transform: rotate(0deg); } 100% { transform: rotate(360deg); } } #mlb2-27858390.ml-form-embedContainer { box-sizing: border-box; display: table; margin: 0 auto; position: static; width: 100% !important; } #mlb2-27858390.ml-form-embedContainer h4, #mlb2-27858390.ml-form-embedContainer p, #mlb2-27858390.ml-form-embedContainer span, #mlb2-27858390.ml-form-embedContainer button { text-transform: none !important; letter-spacing: normal !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper { background-color: #f6f6f6; border-width: 0px; border-color: transparent; border-radius: 4px; border-style: solid; box-sizing: border-box; display: inline-block !important; margin: 0; padding: 0; position: relative; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper.embedPopup, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper.embedDefault { width: 400px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper.embedForm { max-width: 400px; width: 100%; } #mlb2-27858390.ml-form-embedContainer .ml-form-align-left { text-align: left; } #mlb2-27858390.ml-form-embedContainer .ml-form-align-center { text-align: center; } #mlb2-27858390.ml-form-embedContainer .ml-form-align-default { display: table-cell !important; vertical-align: middle !important; text-align: center !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-align-right { text-align: right; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedHeader img { border-top-left-radius: 4px; border-top-right-radius: 4px; height: auto; margin: 0 auto !important; max-width: 100%; width: undefinedpx; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody { padding: 20px 20px 0 20px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody.ml-form-embedBodyHorizontal { padding-bottom: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent { text-align: left; margin: 0 0 20px 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent h4, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent h4 { color: #000000; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 30px; font-weight: 400; margin: 0 0 10px 0; text-align: left; word-break: break-word; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent p, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent p { color: #000000; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px; font-weight: 400; line-height: 20px; margin: 0 0 10px 0; text-align: left; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent ul, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent ol, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent ul, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent ol { color: #000000; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent ol ol, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent ol ol { list-style-type: lower-alpha; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent ol ol ol, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent ol ol ol { list-style-type: lower-roman; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent p a, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent p a { color: #000000; text-decoration: underline; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-block-form .ml-field-group { text-align: left!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-block-form .ml-field-group label { margin-bottom: 5px; color: #333333; font-size: 14px; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-weight: bold; font-style: normal; text-decoration: none;; display: inline-block; line-height: 20px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent p:last-child, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent p:last-child { margin: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody form { margin: 0; width: 100%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-formContent, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow { margin: 0 0 20px 0; width: 100%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow { float: left; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-formContent.horozintalForm { margin: 0; padding: 0 0 20px 0; width: 100%; height: auto; float: left; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow { margin: 0 0 10px 0; width: 100%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow.ml-last-item { margin: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow.ml-formfieldHorizintal { margin: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input { background-color: #ffffff !important; color: #333333 !important; border-color: #cccccc; border-radius: 4px !important; border-style: solid !important; border-width: 1px !important; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px !important; height: auto; line-height: 21px !important; margin-bottom: 0; margin-top: 0; margin-left: 0; margin-right: 0; padding: 10px 10px !important; width: 100% !important; box-sizing: border-box !important; max-width: 100% !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input::-webkit-input-placeholder, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow input::-webkit-input-placeholder { color: #333333; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input::-moz-placeholder, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow input::-moz-placeholder { color: #333333; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input:-ms-input-placeholder, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow input:-ms-input-placeholder { color: #333333; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input:-moz-placeholder, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow input:-moz-placeholder { color: #333333; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow textarea, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow textarea { background-color: #ffffff !important; color: #333333 !important; border-color: #cccccc; border-radius: 4px !important; border-style: solid !important; border-width: 1px !important; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px !important; height: auto; line-height: 21px !important; margin-bottom: 0; margin-top: 0; padding: 10px 10px !important; width: 100% !important; box-sizing: border-box !important; max-width: 100% !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::before { border-color: #cccccc!important; background-color: #ffffff!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input.custom-control-input[type="checkbox"]{ box-sizing: border-box; padding: 0; position: absolute; z-index: -1; opacity: 0; margin-top: 5px; margin-left: -1.5rem; overflow: visible; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::before { border-radius: 4px!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow input[type=checkbox]:checked~.label-description::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox input[type=checkbox]:checked~.label-description::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-input:checked~.custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-input:checked~.custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox input[type=checkbox]:checked~.label-description::after { background-image: url("data:image/svg+xml,%3csvg xmlns='http://www.w3.org/2000/svg' viewBox='0 0 8 8'%3e%3cpath fill='%23fff' d='M6.564.75l-3.59 3.612-1.538-1.55L0 4.26 2.974 7.25 8 2.193z'/%3e%3c/svg%3e"); } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-input:checked~.custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-input:checked~.custom-control-label::after { background-image: url("data:image/svg+xml,%3csvg xmlns='http://www.w3.org/2000/svg' viewBox='-4 -4 8 8'%3e%3ccircle r='3' fill='%23fff'/%3e%3c/svg%3e"); } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-input:checked~.custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-input:checked~.custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-input:checked~.custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-input:checked~.custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox input[type=checkbox]:checked~.label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox input[type=checkbox]:checked~.label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow input[type=checkbox]:checked~.label-description::before { border-color: #000000!important; background-color: #000000!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-label::after { top: 2px; box-sizing: border-box; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::after { top: 0px!important; box-sizing: border-box!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::after { top: 0px!important; box-sizing: border-box!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::after { top: 0px!important; box-sizing: border-box!important; position: absolute; left: -1.5rem; display: block; width: 1rem; height: 1rem; content: ""; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::before { top: 0px!important; box-sizing: border-box!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .custom-control-label::before { position: absolute; top: 4px; left: -1.5rem; display: block; width: 16px; height: 16px; pointer-events: none; content: ""; background-color: #ffffff; border: #adb5bd solid 1px; border-radius: 50%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .custom-control-label::after { position: absolute; top: 2px!important; left: -1.5rem; display: block; width: 1rem; height: 1rem; content: ""; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::before { position: absolute; top: 4px; left: -1.5rem; display: block; width: 16px; height: 16px; pointer-events: none; content: ""; background-color: #ffffff; border: #adb5bd solid 1px; border-radius: 50%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::after { position: absolute; top: 0px!important; left: -1.5rem; display: block; width: 1rem; height: 1rem; content: ""; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::after { position: absolute; top: 0px!important; left: -1.5rem; display: block; width: 1rem; height: 1rem; content: ""; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .custom-radio .custom-control-label::after { background: no-repeat 50%/50% 50%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .custom-checkbox .custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::after { background: no-repeat 50%/50% 50%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-control, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-control { position: relative; display: block; min-height: 1.5rem; padding-left: 1.5rem; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-input, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-input, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-input, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-input { position: absolute; z-index: -1; opacity: 0; box-sizing: border-box; padding: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-label, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-label, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-label, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-label { color: #000000; font-size: 12px!important; font-family: 'Open Sans', Arial, Helvetica, sans-serif; line-height: 22px; margin-bottom: 0; position: relative; vertical-align: top; font-style: normal; font-weight: 700; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-select, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-select { background-color: #ffffff !important; color: #333333 !important; border-color: #cccccc; border-radius: 4px !important; border-style: solid !important; border-width: 1px !important; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px !important; line-height: 20px !important; margin-bottom: 0; margin-top: 0; padding: 10px 28px 10px 12px !important; width: 100% !important; box-sizing: border-box !important; max-width: 100% !important; height: auto; display: inline-block; vertical-align: middle; background: url('https://assets.mlcdn.com/ml/images/default/dropdown.svg') no-repeat right .75rem center/8px 10px; -webkit-appearance: none; -moz-appearance: none; appearance: none; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow { height: auto; width: 100%; float: left; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .ml-input-horizontal { width: 70%; float: left; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .ml-button-horizontal { width: 30%; float: left; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .ml-button-horizontal.labelsOn { padding-top: 25px; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .horizontal-fields { box-sizing: border-box; float: left; padding-right: 10px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow input { background-color: #ffffff; color: #333333; border-color: #cccccc; border-radius: 4px; border-style: solid; border-width: 1px; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px; line-height: 20px; margin-bottom: 0; margin-top: 0; padding: 10px 10px; width: 100%; box-sizing: border-box; overflow-y: initial; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow button { background-color: #004169 !important; border-color: #004169; border-style: solid; border-width: 1px; border-radius: 4px; box-shadow: none; color: #ffffff !important; cursor: pointer; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px !important; font-weight: 700; line-height: 20px; margin: 0 !important; padding: 10px !important; width: 100%; height: auto; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow button:hover { background-color: #333333 !important; border-color: #333333 !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow input[type="checkbox"] { box-sizing: border-box; padding: 0; position: absolute; z-index: -1; opacity: 0; margin-top: 5px; margin-left: -1.5rem; overflow: visible; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description { color: #000000; display: block; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 12px; text-align: left; margin-bottom: 0; position: relative; vertical-align: top; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow label { font-weight: normal; margin: 0; padding: 0; position: relative; display: block; min-height: 24px; padding-left: 24px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow label a { color: #000000; text-decoration: underline; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow label p { color: #000000 !important; font-family: 'Open Sans', Arial, Helvetica, sans-serif !important; font-size: 12px !important; font-weight: normal !important; line-height: 18px !important; padding: 0 !important; margin: 0 5px 0 0 !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow label p:last-child { margin: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedSubmit { margin: 0 0 20px 0; float: left; width: 100%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedSubmit button { background-color: #004169 !important; border: none !important; border-radius: 4px !important; box-shadow: none !important; color: #ffffff !important; cursor: pointer; font-family: 'Open Sans', Arial, Helvetica, sans-serif !important; font-size: 14px !important; font-weight: 700 !important; line-height: 21px !important; height: auto; padding: 10px !important; width: 100% !important; box-sizing: border-box !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedSubmit button.loading { display: none; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedSubmit button:hover { background-color: #333333 !important; } .ml-subscribe-close { width: 30px; height: 30px; background: url('https://assets.mlcdn.com/ml/images/default/modal_close.png') no-repeat; background-size: 30px; cursor: pointer; margin-top: -10px; margin-right: -10px; position: absolute; top: 0; right: 0; } .ml-error input, .ml-error textarea, .ml-error select { border-color: red!important; } .ml-error .custom-checkbox-radio-list { border: 1px solid red !important; border-radius: 4px; padding: 10px; } .ml-error .label-description, .ml-error .label-description p, .ml-error .label-description p a, .ml-error label:first-child { color: #ff0000 !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow.ml-error .label-description p, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow.ml-error .label-description p:first-letter { color: #ff0000 !important; } @media only screen and (max-width: 400px){ .ml-form-embedWrapper.embedDefault, .ml-form-embedWrapper.embedPopup { width: 100%!important; } .ml-form-formContent.horozintalForm { float: left!important; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow { height: auto!important; width: 100%!important; float: left!important; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .ml-input-horizontal { width: 100%!important; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .ml-input-horizontal > div { padding-right: 0px!important; padding-bottom: 10px; } .ml-form-formContent.horozintalForm .ml-button-horizontal { width: 100%!important; } .ml-form-formContent.horozintalForm .ml-button-horizontal.labelsOn { padding-top: 0px!important; } } </style> <div id="mlb2-27858390" class="ml-form-embedContainer ml-subscribe-form ml-subscribe-form-27858390"> <div class="ml-form-align-center "> <div class="ml-form-embedWrapper embedForm"> <div class="ml-form-embedBody ml-form-embedBodyDefault row-form"> <div class="ml-form-embedContent" style=" "> <h4>My report</h4> Beer Money Report: Monthly Report and sites </div> <form class="ml-block-form" action="https://assets.mailerlite.com/jsonp/999177/forms/158706521894553421/subscribe" data-code="" method="post" target="_blank"> <div class="ml-form-formContent"> <div class="ml-form-fieldRow ml-last-item"> <div class="ml-field-group ml-field-email ml-validate-email ml-validate-required"> <!-- input --> <input aria-label="email" aria-required="true" type="email" class="form-control" data-inputmask="" name="fields[email]" placeholder="Email" autocomplete="email"> <!-- /input --> <!-- textarea --> <!-- /textarea --> <!-- select --> <!-- /select --> <!-- checkboxes --> <!-- /checkboxes --> <!-- radio --> <!-- /radio --> <!-- countries --> <!-- /countries --> </div> </div> </div> <!-- Privacy policy --> <!-- /Privacy policy --> <input type="hidden" name="ml-submit" value="1"> <div class="ml-form-embedSubmit"> <button type="submit" class="primary">Subscribe</button> <button disabled="disabled" style="display: none;" type="button" class="loading"> <div class="ml-form-embedSubmitLoad"></div> <span class="sr-only">Loading...</span> </button> </div> <input type="hidden" name="anticsrf" value="true"> </form> </div> <div class="ml-form-successBody row-success" style="display: none"> <div class="ml-form-successContent"> <h4>Thank you!</h4> You have successfully joined the Best Beer Money List </div> </div> </div> </div> </div> <script> function ml_webform_success_27858390() { var = ml_jQuery || jQuery; ('.ml-subscribe-form-27858390 .row-success').show();(‘.ml-subscribe-form-27858390 .row-form’).hide(); }

PlatformAmount EarnedReferral Link
Clickworker21</td><td><a href="https://clickworker.page.link/r2jdqB4M4bBZKeXC7">Join Clickworker</a></td></tr><tr><td><strong>Prime Opinion</strong></td><td>5Join Prime Opinion
ySense15</td><td><a href="https://www.ysense.com/?rb=156010655">Join ySense</a></td></tr><tr><td><strong>YouGov</strong></td><td>10–
GameTester.gg15</td><td><a href="https://gametester.gg/?refId=UU-6817bd3b4c3461c3aa974163">Join GameTester</a></td></tr><tr><td><strong>Aurora Studio</strong></td><td>25Join Aurora Studio
Respondent.io40</td><td><a href="https://app.respondent.io/r/shounakdas-639da7caadd4">Join Respondent</a></td></tr><tr><td><strong>User Interviews</strong></td><td>10Join User Interviews
Miscellaneous5</td><td>-</td></tr><tr><td><strong>Total</strong></td><td><strong>146—

What is Beer Money?

Beer Money refers to small online tasks that pay in dollars (or equivalent) and are not a regular job or freelancing gig. These are low-commitment microtasks, surveys, testing jobs, or opinion panels that pay small amounts, but when done consistently, they add up.

Now, let’s look at the exact platforms I used this month, how much I made from each, and how you can start doing the same.

Proof of my Earning in June 2025

1. Clickworker – 21</strong></h2> <!-- /wp:heading --> <!-- wp:paragraph --> One of the most trusted microtask platforms around, <strong>Clickworker</strong> lets you earn by doing simple tasks like categorization, copywriting, proofreading, and more. <!-- /wp:paragraph --> <!-- wp:list --> <ul class="wp-block-list"><!-- wp:list-item --> <li><strong>Tasks</strong>: Short AI training prompts, small Ai\I tasks, and micro task</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li><strong>Earnings This Month</strong>:21
  • Pro Tips: Download the Clickworker mobile app for mobile-exclusive tasks. Always do the assessments to unlock more tasks.

    • 👉 Sign up with my Clickworker Referral Link

    2. Prime Opinion – 5</strong></h2> <!-- /wp:heading --> <!-- wp:paragraph --> A relatively newer platform but very smooth to use. <strong>Prime Opinion</strong> sends out high-paying surveys with decent frequency. <!-- /wp:paragraph --> <!-- wp:list --> <ul class="wp-block-list"><!-- wp:list-item --> <li><strong>Tasks</strong>: Mostly consumer and market research surveys and sign up offers on offer wall</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li><strong>Earnings This Month</strong>:5
  • Pro Tips: Fill out your profile completely to increase your chances of getting more targeted surveys.

    • 👉 Join Prime Opinion with my Referral Link

    3. ySense – 15</strong></h2> <!-- /wp:heading --> <!-- wp:paragraph --> An all-in-one platform offering surveys, small tasks, and offer walls. It also pays you to sign up on other platforms and apps through offers. <!-- /wp:paragraph --> <!-- wp:list --> <ul class="wp-block-list"><!-- wp:list-item --> <li><strong>Tasks</strong>: Surveys</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li><strong>Earnings This Month</strong>:15
  • Pro Tips: Focus on tasks that pay 1-3.

    • 👉 Join ySense with my Referral Link

    4. YouGov – 10</strong></h2> <!-- /wp:heading --> <!-- wp:paragraph --> <strong>YouGov</strong> is a well-known research company where your opinions help influence political and commercial decisions. They take some time to accumulate enough points, but their surveys are easy. <!-- /wp:paragraph --> <!-- wp:list --> <ul class="wp-block-list"><!-- wp:list-item --> <li><strong>Tasks</strong>: Weekly surveys on politics, brands, social views.</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li><strong>Earnings This Month</strong>:10 (after several weeks of accumulating points)
  • Pro Tips: Stay consistent; Upload amazon prime, Netflix Data points accumulate slowly but surely. They offer gift cards.

    • 5. Game Testing Platforms – 40</strong></h2> <!-- /wp:heading --> <!-- wp:paragraph --> This is where things got exciting. Game testing pays more than regular survey platforms if you're selected. <!-- /wp:paragraph --> <!-- wp:heading {"level":3} --> <h3 class="wp-block-heading">a. <strong>Antidote.gg</strong></h3> <!-- /wp:heading --> <!-- wp:paragraph --> I was invited to test an unreleased football game. The experience was smooth, and the pay was decent. <!-- /wp:paragraph --> <!-- wp:heading {"level":3} --> <h3 class="wp-block-heading">b. <strong>GameTester.gg</strong></h3> <!-- /wp:heading --> <!-- wp:list --> <ul class="wp-block-list"><!-- wp:list-item --> <li><strong>Tasks</strong>: Playtest games in beta stages.</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li><strong>Pro Tips</strong>: Keep your profile updated with your gaming preferences and platform availability.👉 <a href="https://gametester.gg/?refId=UU-6817bd3b4c3461c3aa974163">Join GameTester with my Referral Link</a></li> <!-- /wp:list-item --></ul> <!-- /wp:list --> <!-- wp:heading {"level":3} --> <h3 class="wp-block-heading">c. <strong>Aurora Studio</strong></h3> <!-- /wp:heading --> <!-- wp:list --> <ul class="wp-block-list"><!-- wp:list-item --> <li><strong>Tasks</strong>: AI tasks👉 <a href="https://app.aurorastudio.com/auth/referred?refId=UU-6817bd3b4c3461c3aa974163">Join Aurora Studio via Referral</a></li> <!-- /wp:list-item --></ul> <!-- /wp:list --> <!-- wp:separator --> <hr class="wp-block-separator has-alpha-channel-opacity"/> <!-- /wp:separator --> <!-- wp:heading --> <h2 class="wp-block-heading">6. <strong>Respondent.io -40

    One of the highest-paying opportunities this month came from Respondent.io, a platform where researchers pay you to participate in interviews or usability studies.

    • Tasks: 30–45 min interviews and feedback sessions.
    • Earnings This Month: 40</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li><strong>Pro Tips</strong>: Keep checking project listings daily, apply quickly, and make your profile detailed and professional.</li> <!-- /wp:list-item --></ul> <!-- /wp:list --> <!-- wp:paragraph --> 👉 <a href="https://app.respondent.io/r/shounakdas-639da7caadd4">Join Respondent with my Referral Link</a> <!-- /wp:paragraph --> <!-- wp:separator --> <hr class="wp-block-separator has-alpha-channel-opacity"/> <!-- /wp:separator --> <!-- wp:heading --> <h2 class="wp-block-heading">7. <strong>UserInterviews -10

    Like Respondent, UserInterviews offers remote interviews and studies on a wide range of topics.

    • Tasks: Remote usability testing, marketing feedback, or product reviews.
    • Earnings This Month: 10</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li><strong>Pro Tips</strong>: Apply for as many studies as you can. Approval is competitive.</li> <!-- /wp:list-item --></ul> <!-- /wp:list --> <!-- wp:paragraph --> 👉 <a href="https://www.userinterviews.com/r/nkptjamqa">Sign Up for UserInterviews with Referral</a> <!-- /wp:paragraph --> <!-- wp:separator --> <hr class="wp-block-separator has-alpha-channel-opacity"/> <!-- /wp:separator --> <!-- wp:heading --> <h2 class="wp-block-heading">8. <strong>Miscellaneous Opportunities -5

    These include random small wins from Reddit’s beermoney India subreddit where I grabbed app testing

    How I Managed Time

    You might wonder how I balanced these platforms. I didn’t sit down for hours daily—instead, I checked them during idle moments:

    • Clickworker and ySense were done in between classes or while commuting.
    • Game testing happened on weekends.
    • Interview platforms like Respondent and UserInterviews were pre-scheduled, so I could plan ahead.

    Payment Methods Used

    • PayPal: Most platforms pay via PayPal, which you can link to your Indian bank account using services like Payoneer or Wise.
    • Gift Cards: YouGov, ySense, User Interview also offer Amazon India gift cards

    Tips for Indian Users

    • Create a separate email for these platforms to avoid clutter.
    • Be honest in your responses—many platforms will ban users for inconsistent answers.
    • Join communities on Reddit like r/beermoneyindia to stay updated.
    • Install mobile apps where possible; many tasks are mobile-exclusive.
    • Track earnings using Excel or Notion to stay motivated.

    Final Summary

    Here’s the breakdown of what I earned this month:

    PlatformAmount EarnedReferral Link
    Clickworker21</td><td><a href="https://clickworker.page.link/r2jdqB4M4bBZKeXC7">Join Clickworker</a></td></tr><tr><td><strong>Prime Opinion</strong></td><td>5Join Prime Opinion
    ySense15</td><td><a href="https://www.ysense.com/?rb=156010655">Join ySense</a></td></tr><tr><td><strong>YouGov</strong></td><td>10–
    GameTester.gg15</td><td><a href="https://gametester.gg/?refId=UU-6817bd3b4c3461c3aa974163">Join GameTester</a></td></tr><tr><td><strong>Aurora Studio</strong></td><td>25Join Aurora Studio
    Respondent.io40</td><td><a href="https://app.respondent.io/r/shounakdas-639da7caadd4">Join Respondent</a></td></tr><tr><td><strong>User Interviews</strong></td><td>10Join User Interviews
    Miscellaneous5</td><td>-</td></tr><tr><td><strong>Total</strong></td><td><strong>146—

    Final Thoughts

    If you’re a student, part-timer, or someone looking to build side income online from India, these beer money platforms are legit, low-effort, and flexible. While none of them will make you rich, stacking them consistently can easily fetch you 100-200 every month—or even more with high-paying interviews and game tests.

    Start with one or two platforms from the list, focus on quality, and gradually expand. The more you diversify, the more you earn.

    Why Your SPICE Simulator Is Not Oscillating—and How to Fix It

    Shounak Das
    -
    0
    Why Your SPICE Simulator Is Not Oscillating—and How to Fix It

    Oscillators are fundamental to modern electronics. They generate clock signals in digital systems, drive RF circuits in communication systems, and enable timekeeping in microcontrollers. But if you’ve ever tried simulating an oscillator in SPICE, you may have run into a perplexing issue: the circuit doesn’t oscillate—even though it works in theory and might even function on a physical breadboard. This discrepancy can be deeply frustrating.

    This article explains why your SPICE oscillator might not be oscillating and walks you through practical, technically sound methods to fix the issue. Whether you’re using LTspice, PSpice, Ngspice, Qspice or another simulation tool, the principles are broadly applicable.

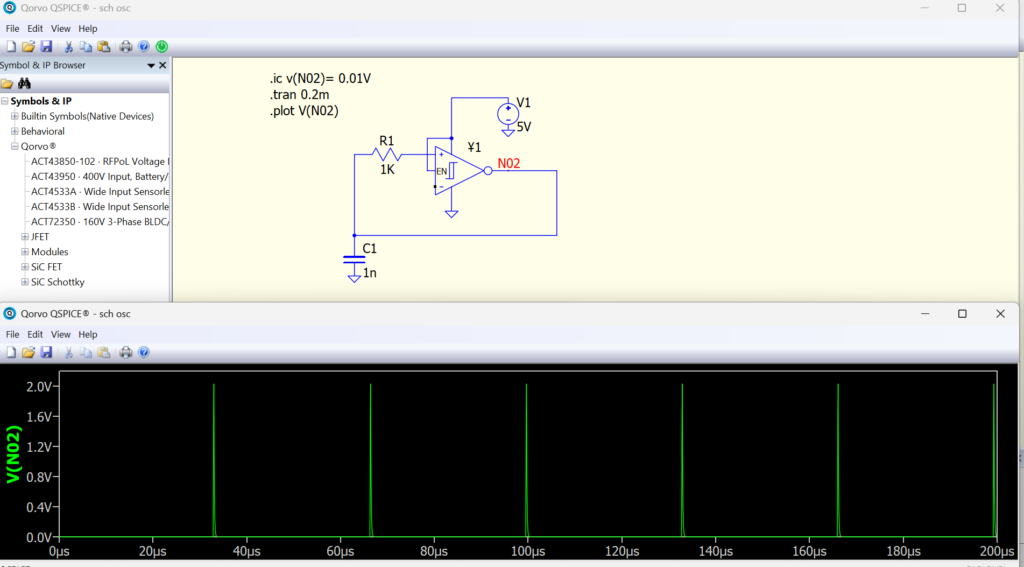
    Understanding the Problem: Why Oscillators Fail in SPICE

    SPICE simulators are designed to analyze circuit behavior under idealized mathematical conditions. This “perfection” becomes a problem when simulating oscillators, which rely on imperfections—like noise, asymmetry, and startup transients—to begin oscillating.

    SPICE Searches for a Stable DC Operating Point

    Before any transient simulation begins, SPICE solves for a steady-state DC operating point. If your oscillator circuit is symmetric and lacks a source of perturbation, the simulator may settle on a static solution where no oscillation occurs. This perfectly balanced condition is mathematically valid but physically unrealistic.

    Oscillation Requires a Kick to Start

    Real-world oscillators don’t start by themselves from perfect stillness. They depend on thermal noise, manufacturing mismatches, or startup voltage fluctuations to push the system out of equilibrium. Since SPICE doesn’t simulate these by default, you have to deliberately inject some form of disturbance.

    Idealized Components Hide Crucial Non-Linearities

    Many oscillator circuits use the non-linear characteristics of real components to stabilize amplitude. For instance, a Wien Bridge oscillator might use diodes or a filament bulb for automatic gain control. If you use ideal op-amp models or transistor models without these non-linearities, the simulator won’t behave like the physical circuit.

    The Barkhausen Criterion: A Theoretical Framework

    Before diving into fixes, it’s helpful to revisit the Barkhausen criterion, which governs sustained oscillation in linear systems:

    1. Loop Gain Must Equal or Exceed Unity: The product of amplifier gain (A) and feedback factor (β) must be at least one (|βA| ≥ 1) for startup. To sustain oscillation, it should stabilize at exactly unity.
    2. Phase Shift Must Be a Multiple of 360°: The signal must reinforce itself after one loop, which requires the total phase shift to be 0° or 360°.

    Meeting both conditions is necessary but not sufficient. Real-world oscillators also rely on non-linear mechanisms to limit amplitude and avoid runaway gain.

    In SPICE, even if you design a circuit that theoretically meets these conditions, it may not start oscillating unless certain additional factors are addressed.

    Causes of Oscillation Failure in SPICE Simulations

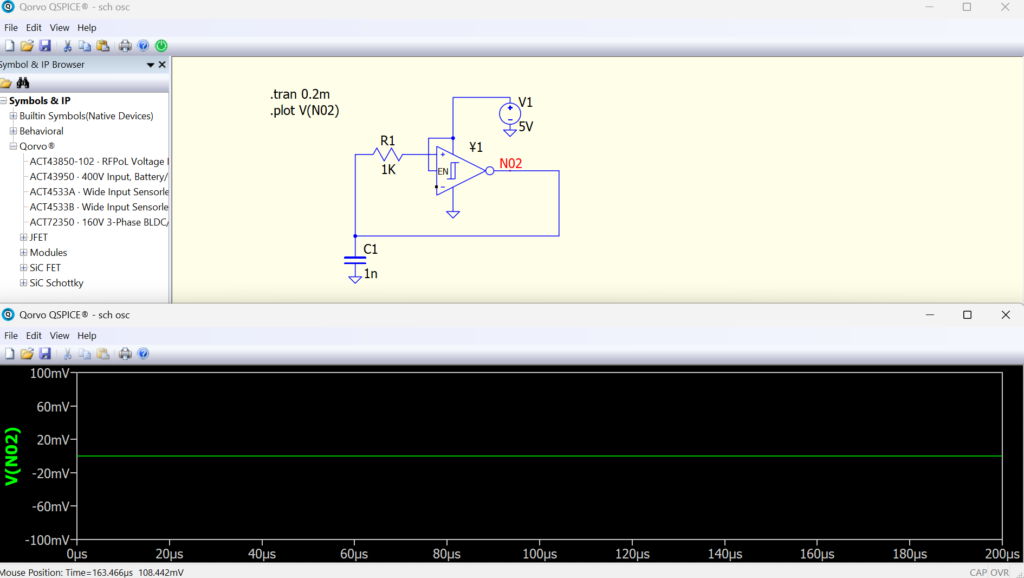
    1. Lack of Startup Perturbation

    In SPICE, without any external disturbance, your oscillator remains stuck in a stable equilibrium. This is the most common reason oscillators fail to start.

    Solution: Inject a small disturbance using one of the following:

    • A PULSE or PWL voltage source on a sensitive node
    • The .IC directive to set initial voltages on capacitors or currents through inductors
    • Behavioral noise sources (e.g., white noise) if supported

    2. Time Step Too Large

    If your simulation uses a large time step, it may completely miss the initial oscillation cycles, especially for high-frequency or high-Q circuits.

    Solution: Set a small dTmax in your .TRAN statement. As a rule of thumb, make it 1/10th to 1/100th of the expected oscillation period.

    .TRAN 1n 10m 0 100n

    3. Ideal or Oversimplified Component Models

    If your amplifier, transistor, or crystal oscillator is modeled too simplistically, critical startup behavior and non-linear amplitude control may be missing.

    Solution:

    • Use manufacturer-provided models instead of generic built-in ones.
    • For op-amp based oscillators, model gain limiting using diodes, JFETs, or behavioral elements.
    • For crystal oscillators, include drive-level dependence and internal parasitics.

    4. Circuit Symmetry and Floating Nodes

    Perfect symmetry can lock the simulator into a non-oscillating state. Additionally, if any node lacks a DC path to ground, convergence problems or failure to start are almost guaranteed.

    Solution:

    • Introduce intentional asymmetry: vary one resistor slightly or apply a tiny offset voltage.
    • Ensure all nodes have a DC path to ground, possibly by adding high-value resistors where needed.

    5. Incorrect Biasing

    If your circuit includes op-amps or active devices, ensure proper biasing. A common mistake is using single-supply op-amps without implementing a virtual ground.

    Solution:

    • Use a voltage divider and buffer to generate a virtual ground.
    • Run an .OP (Operating Point) analysis to check all node voltages.

    6. Unbounded or Excessive Loop Gain

    Too much gain can cause the waveform to grow uncontrollably and clip against supply rails, leading to distorted or square wave outputs.

    Solution:

    • Implement automatic gain control (AGC) using non-linear elements.
    • Use behavioral functions to model amplitude limiting.

    Techniques to Make Oscillators Work in SPICE

    Here’s a detailed strategy for designing oscillator simulations that work reliably.

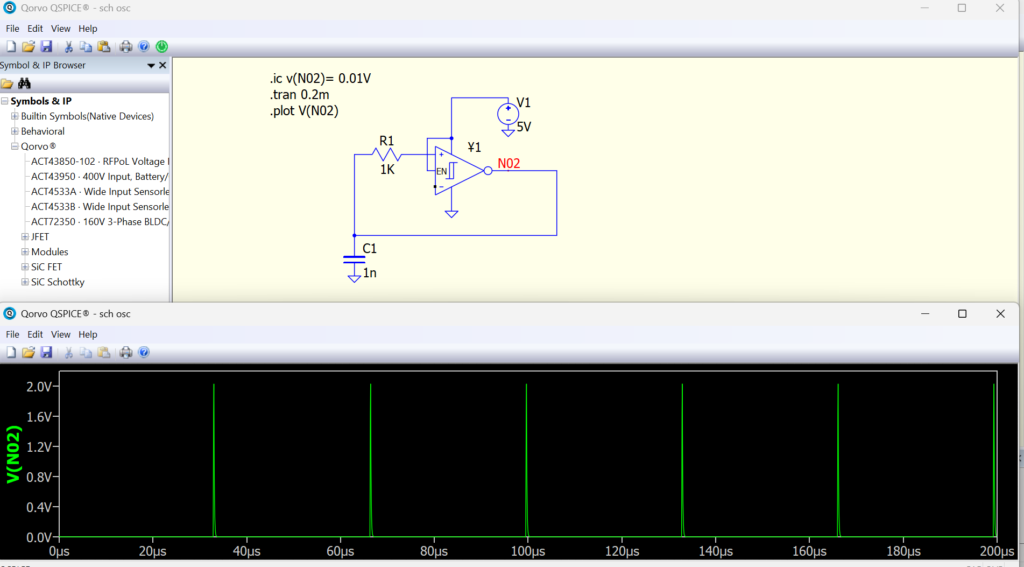
    Use Explicit Initial Conditions

    Use .IC to force initial voltage or current conditions.

    .IC V(n1)=0.05
.TRAN 1n 10m UIC

    The UIC option skips the DC operating point calculation, using your initial conditions directly.

    With initial condition
    Without initial condition

    Ramp the Power Supply

    A simple and effective method is using a piecewise linear (PWL) voltage source to simulate real-world power-up.

    V1 Vcc 0 PWL(0 0 1u 5)

    This gradual ramp can kick the circuit out of its static state.

    Apply a Transient Pulse

    Add a narrow voltage or current pulse at a critical node.

    Vstart n1 0 PULSE(0 1 0 1n 1n 1us 2us)

    Even a brief disturbance is often enough to initiate oscillation.

    Add Noise Sources

    If your SPICE variant supports it, use a behavioral source to inject noise:

    B1 n1 0 V=white(1)

    This mimics thermal or shot noise that initiates oscillation in real circuits.

    Addressing Convergence Issues

    Oscillator circuits are often non-linear and can challenge SPICE’s numerical solvers.

    Use .OPTIONS to tune convergence parameters:

    .OPTIONS RELTOL=0.01 ABSTOL=1n VNTOL=1u GMIN=1n ITL1=500
    • RELTOL: Relative error tolerance
    • ABSTOL/VNTOL: Absolute current/voltage tolerance
    • GMIN: Minimum conductance, helps stabilize matrices
    • ITL1: Iteration limit for DC analysis

    For particularly stubborn circuits, try .NODESET to suggest initial values without fixing them:

    .NODESET V(n1)=1

    Using AC Analysis for Oscillator Stability Verification

    While transient analysis shows whether a circuit will oscillate, AC analysis can predict whether it should oscillate.

    Steps:

    1. Break the feedback loop at a low-impedance point (e.g., op-amp output).
    2. Insert an AC voltage source.
    3. Run .AC analysis to measure gain and phase.

    Check if:

    • Loop gain is >1 at any frequency.
    • Phase shift equals 0° or 360°.

    This pre-simulation verification can save time, especially for high-Q or crystal-based oscillators.

    Special Case: Simulating High-Q Crystal Oscillators

    Crystal oscillators are exceptionally high-Q and take a long time to stabilize, sometimes requiring milliseconds—or even seconds—of simulated time.

    Tips for Crystal Oscillator Simulation:

    • Use accurate models that include shunt capacitance and series RLC.
    • Inject an initial voltage across the crystal to promote startup.
    • Limit the simulation time step aggressively.
    • Consider modeling drive-level dependence if startup amplitude varies with load.

    Troubleshooting Checklist

    CategoryChecklist Item
    Design ValidationDoes the loop gain > 1 and phase shift = 360° at the target frequency?
    Is every node correctly biased and connected?
    Startup ConditionsHave you added .IC, .NODESET, or a startup pulse?
    Is the power supply ramped using a PWL source?
    Component ModelsAre you using realistic, non-ideal models for transistors and op-amps?
    Is AGC implemented or are amplitude-limiting elements present?
    Simulation SetupHave you set a small dTmax in .TRAN?
    Are convergence parameters optimized for non-linear behavior?
    DebuggingHave you simplified the circuit to verify sub-blocks individually?
    Have you confirmed correct operation with .OP and .AC analyses?

    Conclusion: Reliable Oscillator Simulation in SPICE Is Achievable

    SPICE is a powerful tool, but it’s only as effective as the realism you build into your simulation. Oscillators, in particular, challenge the simulator’s assumptions and force you to bridge the gap between ideal math and real-world behavior.

    To simulate oscillators successfully:

    • Inject startup energy intentionally.
    • Model non-linearity for amplitude control.
    • Fine-tune simulator settings for convergence and time resolution.
    • Use advanced analysis techniques to validate designs before full transients.

    Simulating oscillators isn’t just about making SPICE “work.” It’s an exercise in deepening your understanding of both circuit behavior and simulation theory. With the right tools and techniques, you can simulate even complex oscillator circuits with high fidelity.

    Capacitive Soil Moisture Sensor

    Shounak Das
    -
    0

    1.1. Introduction

    This document provides detailed information for the assembly, programming, and operation of the Improved Capacitive Soil Moisture Sensor. This sensor is designed to provide a more reliable and durable alternative to common resistive soil moisture sensors by measuring the dielectric constant of the soil, which is directly proportional to its water content.

    The sensor is controlled by an ATtiny85 microcontroller and communicates with a master device over the I2C protocol, making it easy to integrate into a wide variety of projects, including automated watering systems, environmental monitoring stations, and IoT applications.

    Schematic Breakdown

    1.2. Key Features

    • Capacitive Sensing: Avoids electrode corrosion for longer sensor life and more stable readings.
    • ATtiny85 Microcontroller: A low-power, cost-effective, and powerful core for sensor operation.
    • I2C Interface: Allows for simple communication with a master device and supports connecting multiple sensors on a single bus (daisy-chaining).
    • Onboard Logic: The sensor handles the measurement process internally and outputs a processed digital value.
    • ISP Header: Allows for easy in-system programming of the microcontroller.

    2. Hardware

    2.1. Theory of Operation

    The sensor functions as a capacitor where the two probes (J4, J5) act as the capacitor plates and the surrounding soil acts as the dielectric medium. The principle is based on the fact that water has a much higher dielectric constant than dry soil.

    The measurement process is as follows:

    1. The ATtiny85 microcontroller (U1) uses a digital pin (PB4) to charge the sensor probe (J4) through resistor R1.
    2. The pin’s state is then flipped, allowing the charge to dissipate through the soil to the other probe (J5).
    3. The ATtiny85’s analog-to-digital converter (ADC) on pin PB3 measures the time it takes for the voltage to fall below a certain threshold.
    4. This discharge time is directly proportional to the capacitance of the soil.
      • Wet Soil: Higher capacitance -> Slower discharge -> Longer time measurement.
      • Dry Soil: Lower capacitance -> Faster discharge -> Shorter time measurement.
    5. The measured time is then mapped to a digital value and made available over the I2C bus.

    2.2. Schematic Breakdown

    The circuit is designed for simplicity and efficiency.

    • U1 (ATtiny85): The core of the sensor. It controls the charge/discharge cycle, measures the time, and handles I2C communication.
    • J4, J5 (Sensor Probes): These are the connections for the capacitive probes that will be inserted into the soil.
    • C1 (10uF): A decoupling capacitor to stabilize the power supply to the ATtiny85.
    • R1, R2 (Resistors): These form part of the RC oscillator circuit used for the measurement. Their values affect the sensitivity and range of the sensor.
    • R3, R4 (2.2kΩ): Pull-up resistors for the I2C communication lines (SDA and SCL). These are required for the I2C protocol to function correctly.
    • J1, J2 (I2C/Power Connectors): Standard 4-pin headers for providing power (+3.3V, GND) and I2C communication (SDA, SCL).
    • J3 (ISP Header): A 2×3 pin header for In-System Programming, allowing you to upload firmware to the ATtiny85 without removing it from the board.
    • TP1, TP2 (Test Points): Provide easy access for debugging and verifying voltage levels.

    2.3. Bill of Materials (BOM)

    No.QuantityDesignatorFootprintValue
    12C1, C2Capacitor, SMD10uF
    22J1, J2Conn_01x04_MountingPin4-pin Header
    31J3AVR-ISP-62×3 Header
    42J4, J5Conn_01x011-pin Header
    52R1, R2Resistor, SMD 08051MΩ (Typical)
    62R3, R4Resistor, SMD 08052.2kΩ
    72TP1, TP2TestPointTest Point
    81U1SOIC-8ATtiny85

    Note: Values for R1 and R2 can be experimented with to adjust sensor sensitivity.

    3. Firmware

    3.1. Programming the ATtiny85

    The firmware for the ATtiny85 needs to be uploaded via the ISP header (J3). You will need an AVR programmer, such as a USBasp, or you can configure an Arduino Uno as an ISP.

    Connections for Arduino as ISP:

    • Connect the Arduino’s 5V/3.3V and GND to the sensor’s VCC and GND.
    • Connect Arduino pins 13, 12, 11, and 10 to the sensor’s SCK, MISO, MOSI, and RESET pins on the ISP header, respectively.

    Software:

    • Use the Arduino IDE with the ATtinyCore board manager installed.
    • Select “ATtiny25/45/85” as the board, “ATtiny85” as the processor, and your programmer of choice.
    • Burn the bootloader (to set the correct fuses, e.g., for the internal 8MHz clock).
    • Upload the sensor sketch.

    3.2. Logic Flow

    The firmware should perform the following steps in a loop:

    1. Initialize: Set up pin modes and start the I2C communication interface with a unique device address.
    2. Charge: Set the charge pin (PB4) to HIGH to charge the probe.
    3. Discharge & Measure: Set the charge pin to INPUT (high impedance) and start a timer. Continuously read the analog pin (PB3) until its value drops below a predefined threshold. Stop the timer.
    4. Store Value: The elapsed time is the raw moisture reading. Store this value in a variable that can be accessed via I2C.
    5. I2C Request Handler: Set up an interrupt service routine (ISR) that listens for requests from the I2C master. When a request is received, send the stored moisture value back to the master.
    6. Delay: Wait for a short period before taking the next measurement to conserve power and prevent self-heating.

    3.3. I2C Communication

    • Default Address: The firmware should be programmed with a default I2C address (e.g., 0x2A). If you plan to daisy-chain sensors, you must program each one with a unique address.
    • Data Format: The master device can request data from the sensor’s address. The sensor will respond with a 2-byte integer representing the raw moisture reading (0-1023).

    4. Integration and Usage

    4.1. Connecting to a Master Device (e.g., Arduino)

    1. Connect the sensor’s VCC and GND pins to the Arduino’s 3.3V and GND pins.
    2. Connect the sensor’s SDA pin to the Arduino’s A4 pin (SDA).
    3. Connect the sensor’s SCL pin to the Arduino’s A5 pin (SCL).
    4. In your Arduino sketch, use the Wire.h library to request data from the sensor’s I2C address.

    4.2. Calibration

    For accurate readings, a two-point calibration is recommended.

    1. Dry Reading: Place the sensor in completely dry soil and record the raw value from the sensor. This is your dryValue.
    2. Wet Reading: Submerge the sensor in a glass of water and record the raw value. This is your wetValue.
    3. Mapping: Use these two values in your master device’s code to map the sensor’s output to a percentage (0-100%).

    4.3. Daisy-Chaining

    You can connect multiple sensors to the same I2C bus.

    • Ensure all sensors are connected in parallel (all SDA lines together, all SCL lines together).
    • Crucially, each sensor must be programmed with a unique I2C address.
    • The master device can then poll each sensor individually by addressing it specifically.

    Sora Video Generator for Free

    Shounak Das
    -
    0
    Sora Video Generator for Free

    Artificial intelligence is changing the way we create content. From images and music to stories and now even videos, AI tools are opening up creative opportunities for everyone. One of the most exciting tools in this space is OpenAI’s Sora, a video generator that can turn a simple text prompt into a five-second video clip.

    The best part? You can now use Sora for free through the Bing mobile app—no subscription, no complicated setup.

    In this post, we’ll explain what the Sora video generator is, how you can use it for free on your phone, and some tips for getting the best results from it.

    What Is Sora and Why Is It a Big Deal?

    Sora is a video generation model developed by OpenAI. It takes written prompts and turns them into short video clips that look realistic and often cinematic. This kind of tool was previously only available to large studios or researchers, but now it’s available to regular users—thanks to Microsoft’s partnership with OpenAI.

    In June 2025, Microsoft quietly rolled out a new feature in the Bing mobile app called Video Creator, powered by Sora. This allows users to create five-second vertical videos using nothing more than a short sentence. And yes—it’s free.

    How to Access Sora Video Generator for Free (Step-by-Step)

    If you want to start generating videos right now, here’s how to do it:

    1. Install the Bing App on Your Phone

    Start by downloading the Microsoft Bing app from the Google Play Store (Android) or the App Store (iOS). Make sure it’s the official version published by Microsoft.

    2. Sign In with a Microsoft Account

    You’ll need a free Microsoft account to access the video creation features. If you don’t have one, it takes less than a minute to set up.

    Signing in also enables Microsoft Rewards, which lets you earn points for using Bing. These points can be used to speed up video generation later.

    3. Open the Video Creator

    Once inside the Bing app:

    • Tap the “Bing” button or menu icon.
    • Look for a section called “Video Creator” or type a prompt like “Create a video of…” into the search bar.

    This will launch the video generation interface powered by Sora.

    4. Write a Prompt

    Type in a short, descriptive sentence of what you want to see. For example:

    cinematic video of a man with egg in a deserted island, Ray tracing, cinematic light

    The more specific your prompt, the better the result.

    5. Choose Standard or Fast Creation

    By default, video generation is free and runs on a standard speed, which may take a little time depending on demand.

    If you want faster results, you can use Microsoft Rewards points. You get 10 fast generations to start. After that, it costs 100 points per fast render.

    6. Wait for Your Video to Generate

    You can queue up to three videos at once. Once a video is ready, you’ll get a notification and can preview, download, or share it.

    Videos stay saved for 90 days, so be sure to download anything you want to keep long term.

    Features and Benefits

    Let’s take a quick look at why using Sora on Bing Mobile is worth trying:

    • Totally free for basic video generation
    • No need for ChatGPT Plus or any paid subscription
    • Simple user interface—ideal for beginners
    • Generate up to 5-second videos in portrait format (great for Reels or TikToks)
    • Download and share videos directly from your phone
    • Use Microsoft Rewards for faster results without paying real money

    How to Write Better Prompts

    To get the best videos out of Sora, the prompt you write matters a lot. Here are a few tips:

    • Be descriptive: Include details like the subject, setting, lighting, and motion.
      • Example: “A lone astronaut walking on Mars at sunset, dust blowing in the wind, cinematic style.”
    • Use camera terms: Words like “close-up,” “wide-angle,” or “aerial view” can help the AI visualize better.
    • Mention mood or tone: Try prompts like “dark and eerie forest” or “cheerful city street during spring.”
    • Add motion elements: “Birds flying,” “waves crashing,” or “car drifting” all bring action into your scene.
    • Keep experimenting: If one prompt doesn’t work well, try rephrasing it or adding more detail.

    What Can You Use It For?

    The Sora video generator isn’t just a cool tool—it has lots of practical uses:

    1. Content Creation for Social Media

    Generate quick, visually appealing videos for TikTok, Instagram Stories, or YouTube Shorts.

    2. Marketing and Ads

    Create short product visuals or teaser clips for new campaigns—without needing a video team.

    3. Education and Learning

    Explain concepts using short clips, like showing the water cycle or a historical event.

    4. Creative Projects and Storytelling

    Use it to bring parts of your stories or poems to life visually.

    5. Idea Prototyping

    Visualize a scene, environment, or action before committing to full-scale video production.

    Are There Any Limitations?

    Yes, there are a few things to keep in mind:

    • Only 5-second videos: Sora currently generates very short clips. Longer videos are not supported yet.
    • Vertical (portrait) format only: 9:16 videos are best for phones and social media. Horizontal format is coming soon.
    • Basic quality: These videos are good for fun or prototyping, but not yet ready for film-level quality.
    • No NSFW or harmful content allowed: Prompts are filtered for safety.
    • Rendering can be slow: Especially if you don’t use points. Be patient or redeem Microsoft Rewards for speed.

    Why Microsoft Made It Free

    Microsoft’s goal is clear: make AI tools accessible to everyone, not just tech pros or businesses. By bringing Sora to Bing Mobile, they’re:

    • Expanding the reach of OpenAI’s tech
    • Giving users a reason to try the Bing ecosystem
    • Helping casual users experiment with video creativity

    This also sets them apart from competitors like Google’s Veo and shows how serious they are about owning the AI space.

    What’s Coming Next?

    According to Microsoft and OpenAI, the following updates are planned:

    • Desktop version: Soon you’ll be able to access Video Creator from Bing.com on your computer.
    • Horizontal (16:9) video format: For traditional YouTube or widescreen uses.
    • Longer videos: Possibly beyond 5 seconds in future versions.
    • Better prompt control and editing options.

    Final Thoughts

    The integration of Sora into Bing Mobile is a big step forward for free AI tools. Whether you’re a student, content creator, marketer, or just curious about AI, you can now try powerful video generation technology from your phone—for free.

    There’s no need to sign up for ChatGPT Plus or install complex software. Just download Bing Mobile, write a prompt, and let Sora bring your words to life in video form.

    If you haven’t tried it yet, now is a great time to explore the future of video creation

    Empowering Careers: How People with Disabilities Can Use Technology to Thrive Professionally

    Shounak Das
    -
    0
    Empowering Careers: How People with Disabilities Can Use Technology to Thrive Professionally

    Modern technology continues to reshape the workforce in radical ways, opening doors for many who were previously marginalized or underserved. For people with disabilities, digital innovation has become more than just a convenience—it’s a pathway to economic independence, self-expression, and professional fulfillment. From assistive tools that accommodate physical or cognitive challenges to platforms that offer flexible remote work, the possibilities are expansive. Whether you’re seeking higher education, launching a home-based business, or entering the job market for the first time, technology can be a powerful equalizer.

    Launch a Home-Based Business

    Working from home isn’t just a pandemic-era convenience—it’s a viable long-term strategy, especially for individuals with disabilities. E-commerce, consulting, coaching, and digital services like graphic design or freelance writing can all be managed from a home office. This eliminates the need for expensive or inaccessible transportation and offers full control over your work environment. Technology platforms like Etsy, Shopify, or Upwork make it easy to market and sell your products or services to a global audience. With social media and digital marketing tools, entrepreneurs can build loyal customer bases and grow sustainable income streams on their own terms.

    The Value of Earning an Online Degree

    One of the most impactful ways to turn personal ambition into career advancement is through online degree programs. These platforms often come with customizable learning tools that accommodate various needs, such as visual enlargement, voice navigation, or real-time captioning. They also eliminate the need for commuting, which can be both physically and financially taxing. For people with disabilities, this means access to the same educational opportunities as everyone else, on terms that align with their lifestyle. An accredited MBA program, for example, equips you with skills in leadership, strategic planning, financial management, and data-driven decision-making to excel in diverse business environments.

    Tech-Enabled Job Hunting

    Finding the right job has historically been more difficult for individuals with disabilities, but tech is helping to bridge that gap. Online job boards that filter for disability-friendly employers, such as AbilityJobs and Inclusively, help job seekers find workplaces that value accessibility and inclusion. Artificial intelligence can assist in crafting optimized resumes and cover letters that get noticed by hiring algorithms. Virtual interviews conducted via accessible platforms further level the field, removing many of the physical and logistical challenges of in-person meetings. Many companies now highlight their commitment to accessible hiring, and tools like LinkedIn allow you to network with recruiters and professionals who support inclusive employment.

    Assistive Technology to Bridge the Functional Gap

    Perhaps the most transformative aspect of technology for people with disabilities is assistive tech. From screen readers like JAWS and NVDA to voice-to-text software like Dragon NaturallySpeaking, these tools make it possible to interact with digital environments in ways that suit your specific needs. Ergonomic keyboards, eye-tracking systems, and adaptive mice provide alternatives to traditional input methods. For neurodivergent individuals, focus-enhancing tools like noise-canceling apps and task managers aid in concentration and organization. These advancements make it easier not just to access job opportunities, but to perform well and grow in a professional setting.

    Find Gigs on Your Own Terms

    Freelancing is often overlooked as a viable career track, but it offers considerable autonomy, especially for those navigating accessibility challenges. Platforms like Fiverr, Freelancer, and Toptal allow you to build a portfolio and choose projects that align with your strengths and limitations. You set your own rates, hours, and workload, which is ideal for managing energy levels or medical routines. Plus, remote gig work often means you’re judged primarily on output rather than physical presence. It’s a great way to build experience, earn income, and potentially transition into larger roles or full-time contracts.

    Virtual Communities: Mentorship and Advocacy

    One often undervalued resource is the online community of professionals with disabilities. Forums, Slack groups, Facebook pages, and nonprofits like the National Organization on Disability offer support, job leads, and mentorship. Being part of a community that understands your experiences can build confidence and help you stay informed about new tools and opportunities. These groups can also be platforms for advocacy, where you can help shape better hiring practices or product design through feedback and user testing. It’s a powerful reminder that career growth doesn’t have to be solitary; it can be collective and empowering.

    Cultivate Focus and Calm in a Busy Work Life

    Career success often hinges not just on technical skill, but on emotional clarity and mental balance—and that’s where meditation apps come in. Platforms like Insight Timer, Headspace, and Balance provide guided meditations that help you manage stress, improve concentration, and reset your mood during workdays. These tools are especially helpful when navigating high-pressure environments or balancing health concerns alongside professional goals. By integrating mindfulness into your daily rhythm, you build a foundation of calm that supports sharper thinking and greater resilience on the job.

    People with disabilities have always been capable, but systemic barriers too often dictated the narrative. Now, technology is shifting that story, turning previously closed doors into gateways of opportunity. Whether you want to earn a degree, start your own business, find the right employer, or simply work smarter with assistive tools, there’s never been a better time to embrace digital empowerment. With the right strategy and support, technology isn’t just a workaround—it’s your competitive edge.

    Dive into the wonders of science and technology with The Science 360, where curiosity meets innovation through engaging articles and insights!

    How to Create Stunning Comics Using ChatGPT and GPT4o Image Generation

    Shounak Das
    -
    0
    How to Create Stunning Comics Using ChatGPT and GPT4o Image Generation

    In today’s digital age, the process of comic creation is evolving rapidly. Artists and writers alike are discovering the power of artificial intelligence to bring their creative visions to life. If you’re wondering how to make comics from doodles like I did using ChatGPT and GPT-4 image generation, you’re in the right place. In this guide, I’ll walk you through the entire process—from sketching your initial comic panels to transforming your basic doodles into modern, polished illustrations that tell a story.

    The Rise of AI in Comic Creation

    With advancements in AI and machine learning, traditional comic creation methods have been enhanced with powerful digital tools. Platforms like ChatGPT, especially the latest GPT-4 version, have opened new doors in artistic creation. These tools allow creators to brainstorm ideas, refine dialogue, and even generate descriptive texts that guide the illustration process. The integration of ChatGPT with image generation systems is a game changer, making the artistic journey more accessible and efficient.

    first and final output

    Why Use ChatGPT and GPT-4 for Comics?

    1. Speed and Efficiency: Instead of spending hours refining scripts or searching for inspiration, ChatGPT can generate creative dialogue, narratives, and even scene descriptions in seconds.
    2. Enhanced Creativity: By incorporating AI into your workflow, you can experiment with different storylines, character dialogues, and visual concepts without starting from scratch.
    3. Consistency in Style: With image generation models like GPT-4, you can maintain a consistent artistic style across all your panels, ensuring that your comic looks professional and cohesive.
    4. Cost-Effective: AI tools can reduce the reliance on expensive software or hiring multiple creative professionals, making comic creation more budget-friendly.

    Steps in short:

    • Start with a Doodle: Sketch your comic panels with basic ideas and layouts.
    • Craft a Narrative: Use ChatGPT to generate creative storylines and dialogue tailored to your doodle’s theme.
    • Refine Your Script: Edit and enhance the text to ensure a natural flow and engaging humor.
    • Enhance the Visuals: Use GPT-4 image generation to transform your doodle into a polished, modern comic panel.
    • Integrate Text and Graphics: Position dialogue and narrative text carefully on your enhanced images.
    • Apply Final Touches: Adjust fonts, colors, and layout for a cohesive, professional look.
    • Publish and Share: Optimize for SEO and share your finished comic on social media and digital platforms for maximum reach.

    Step-by-Step Guide to Creating Comics Using ChatGPT and GPT-4 Image Generation

    Let’s break down the process of turning your doodles into a modern comic strip, focusing on how to integrate ChatGPT into your creative workflow.

    1. Start with a Doodle

    Every great comic begins with a simple idea, often sketched as a doodle. Your initial doodle is more than just rough art—it’s a blueprint of what your story will look like. The sketch doesn’t have to be perfect; its purpose is to help you visualize the layout of panels, characters, and key elements in the scene.

    Tip: Use paper and pencil or a digital drawing tablet to keep your doodle. This step is all about brainstorming, so keep it loose and imaginative.

    Doodle comics

    2. Develop Your Storyline and Dialogue Using ChatGPT

    Once you have your basic doodle, the next step is to craft a compelling storyline and dialogue that will bring your comic to life. Here’s how ChatGPT comes into play:

    • Generate Ideas: Ask ChatGPT for creative ideas based on your doodle’s theme. For instance, if your doodle shows a futuristic robot, prompt ChatGPT with “Write a humorous scene featuring a robot with unexpected quirks.”
    • Script Development: Develop your narrative by providing ChatGPT with an outline. You can specify details such as panel descriptions, character actions, and dialogue snippets.
    • Editing and Refinement: Use ChatGPT to refine your dialogue and ensure it flows naturally. The model can suggest alternative phrasings or jokes to make your comic even more engaging.

    Example Prompt:

    “ChatGPT, help me write a comic script where a futuristic robot, designed for handling complex tasks, hilariously struggles with simple ones. The comic should have two panels with a modern vibe, and the tone should be light and humorous.”

    ChatGPT will output dialogue and narrative elements that you can incorporate directly into your comic.

    3. Enhance Your Doodle with GPT-4 Image Generation

    After refining your script and storyline, it’s time to focus on the visuals. GPT-4’s image generation capabilities allow you to transform your initial doodle into a polished comic panel. Here’s how to do it:

    • Upload Your Doodle: Start by scanning or taking a clear photo of your doodle. Then, feed the image into the GPT-4 image generation tool.
    • Apply Filters and Enhancements: The tool can apply modern filters, add color, and even incorporate digital effects to enhance your sketch. This step turns your rough drawing into a vibrant comic panel.
    • Adjust for Consistency: If your comic consists of multiple panels, ensure that the same style and color palettes are used throughout. GPT-4’s advanced algorithms help maintain stylistic uniformity, giving your comic a professional, cohesive look.
    final comics

    Tip: Experiment with different enhancements until you achieve the modern, clean aesthetic that aligns with your creative vision. Don’t be afraid to iterate several times until you are satisfied with the outcome.

    4. Integrate Text and Final Touches

    Now that you have your polished visuals and carefully crafted script, it’s time to bring them together. Here’s how to integrate the text with your images effectively:

    • Text Placement: Decide where the dialogue and narrative text should appear on your panels. Ensure that the text doesn’t cover important visuals. Tools often allow you to position, adjust fonts, and resize your text boxes.
    • Choosing the Right Fonts: For a modern look, select fonts that are clean and easy to read. Avoid overly decorative fonts that could distract from the artwork.
    • Final Edits: Review the entire comic for flow, ensuring that the narrative and visual elements complement each other. Make any necessary changes to the dialogue or images to maintain consistency and enhance readability.

    5. Publish and Share Your Comic

    After completing your comic, the final step is to share your creation with the world. Here are some tips for a successful launch:

    • SEO Optimization: When uploading your comic online, create SEO-friendly titles and descriptions. Use keywords like “ChatGPT comic creation,” “GPT-4 image generation comics,” and “AI comic art” to drive organic traffic.
    • Social Media: Share your comic on social media platforms like Instagram, Twitter, and Facebook. Use relevant hashtags to reach a wider audience.
    • Blog Posts and Portfolios: Write blog posts explaining your creative process, as well as showcasing your art. An in-depth behind-the-scenes post can attract fellow artists and enthusiasts.
    • Online Art Communities: Engage with communities on platforms like DeviantArt or Reddit’s comic creation forums. Feedback from fellow creators can provide valuable insights and help you improve your work.

    Benefits of Using AI in Comic Creation

    Unlocking New Creative Possibilities

    AI offers a new realm of possibilities for creative professionals. By combining the storytelling capabilities of ChatGPT with the visual power of GPT-4 image generation, comic creators can experiment with innovative ideas and bring visually stunning narratives to life. This fusion of text and image creation streamlines the process and provides tools to overcome traditional artistic hurdles.

    Increased Productivity and Efficiency

    For many creators, the creative process can sometimes be time-consuming and repetitive. AI tools not only speed up brainstorming sessions but also help refine ideas, making the entire process more efficient. With ChatGPT generating rich dialogue and GPT-4 enhancing your doodles, you can produce high-quality comics at a fraction of the time compared to traditional methods.

    Bridging the Gap Between Art and Technology

    One of the most exciting aspects of this technology is the way it democratizes art. Artists who may not have extensive technical drawing skills can still create compelling narratives and visuals using AI assistance. This integration encourages collaboration between technology and art, resulting in unique creations that push the boundaries of digital storytelling.

    Tips and Best Practices

    Experiment with Different Styles

    Don’t be afraid to experiment with various art styles and narrative tones. The flexibility of GPT-4 allows you to iterate on your design quickly. Whether you’re aiming for a minimalist comic strip or a highly detailed graphic novel style, adjusting the settings can help you find the perfect blend.

    Leverage Feedback Loops

    Engage with your audience for feedback. Use social media polls, online forums, or direct comments on your blog post to learn what works and what doesn’t. Continuous feedback helps improve your future projects and builds a loyal following of fans who appreciate your innovative approach to comic creation.

    Keep Up with AI Advancements

    The fields of AI and digital art are rapidly evolving. Stay updated with the latest tools and techniques by following AI research updates and joining online communities focused on digital storytelling and comic creation. Regularly experimenting with new features can provide you with fresh ideas and improvements to your creative process.

    Conclusion

    The integration of ChatGPT and GPT-4 image generation in comic creation is transforming the way we approach digital art. With these tools, even a simple doodle can be turned into a sophisticated, modern comic strip that captivates audiences. By blending creative storytelling with innovative AI technology, artists can explore new territories in digital expression and set their work apart in an ever-evolving landscape.

    If you’re excited about the potential of these tools and eager to try them out, start by sketching your ideas, fine-tuning your narrative with ChatGPT, and then let GPT-4 elevate your doodles into beautiful, modern visuals. The world of comic creation is no longer limited by traditional methods—it’s an open canvas ready for you to explore.

    How to Create FREE Ghibli Style Images on ChatGPT

    Shounak Das
    -
    0
    How to Create FREE Ghibli Style Images on ChatGPT

    If you’ve been scrolling through social media lately, you’ve probably seen the explosion of Studio Ghibli-style images everywhere. These charming, anime-inspired portraits have taken the internet by storm, with everyone from celebrities to your next-door neighbor transforming their photos into magical Ghibli artwork. While ChatGPT Plus subscribers ($20/month) have been leading this trend, I’ve discovered several completely free alternatives that deliver similar results. Let me walk you through exactly how to create these enchanting images without spending a rupee.

    What’s the Ghibli Style Image Trend All About?

    Studio Ghibli is a renowned Japanese animation studio founded by Hayao Miyazaki, known for beloved films like “Spirited Away,” “My Neighbor Totoro,” and “Howl’s Moving Castle”12. Their distinctive artistic style features soft pastel colors, meticulous details, and a dreamy, whimsical quality that has captivated audiences worldwide.

    The recent trend began when OpenAI rolled out its GPT-4o update, which included an enhanced image generator capable of transforming ordinary photos into Ghibli-inspired artwork14. While initially limited to paying subscribers, there are now ways for everyone to join the fun.

    Free Methods to Create Ghibli-Style Images

    1. Free Access to ChatGPT (Limited)

    According to recent reports, ChatGPT allows free users to generate up to three Ghibli-style images before requiring a subscription10. To try this limited option:

    1. Open the latest version of ChatGPT
    2. Tap the three-dot icon on the prompt bar
    3. Select the “Image” option
    4. Provide a detailed prompt describing your desired Ghibli-style image1214

    2. Using Gemini AI

    Google’s Gemini AI offers a fantastic free alternative for creating Ghibli-style images:

    1. Go to the Gemini AI platform and log in with your Google account
    2. In the chat box, describe the image you want to create in detail
    3. Submit your prompt and wait for the AI to generate your image
    4. Download and share your creation10

    This method works best when you provide specific details about what you want in your Ghibli-style image.

    3. Transform Images with Grok

    Grok, developed by xAI, has emerged as another excellent free option:

    1. Visit the Grok website or app
    2. Upload your image by clicking on the paper clip icon
    3. Ask Grok to “Ghiblify” the image or “transform this into Studio Ghibli style”
    4. Download your Ghibli-style creation when it’s ready1012

    Users report that while Grok’s results might not match ChatGPT Plus’s precision, they’re more than adequate for personal use and social media sharing.

    4. Third-Party AI Image Generators

    Several other platforms can create Ghibli-style images without cost:

    • Craiyon: A free AI image generator accepting text prompts
    • Playground AI: Offers both text-to-image and image transformation features
    • Deep AI: Provides style transfer capabilities that can mimic the Ghibli aesthetic14

    For these platforms, try prompts like “Create an image in the style of Japanese hand-drawn animation showing [your description]” or upload an image and request a stylistic transformation.

    Note that this limited access might not be available to all users yet, as the feature is still rolling out gradually.

    Tips for Getting Better Results

    No matter which platform you use, these tips will help improve your Ghibli-style transformations:

    Be Specific in Your Prompts

    Instead of simply requesting “Ghibli style,” try more descriptive prompts like:

    • “Transform this image into a hand-drawn illustration with soft colors and detailed backgrounds inspired by Japanese animated films”
    • “Convert this photo to resemble the artistic style seen in Miyazaki’s animated works”13

    Work Around Copyright Restrictions

    Many users have reported receiving content policy violation messages when directly mentioning “Studio Ghibli”711. Try these alternatives:

    • “In the style of Hayao Miyazaki”
    • “Japanese anime aesthetic with painterly backgrounds”
    • “Dreamy animation style with pastel colors”13

    Focus on Key Style Elements

    For the most authentic Ghibli look, emphasize:

    • Soft, muted color palettes
    • Detailed natural elements (clouds, grass, trees)
    • Warm, gentle facial expressions
    • Whimsical, dreamlike qualities12

    Troubleshooting Common Issues

    If you encounter problems with generating Ghibli-style images, try these solutions:

    Content Policy Restrictions

    Some platforms restrict certain image types or subjects. Users have reported issues with animal photos in particular7. Try:

    • Using human subjects instead of animals
    • Modifying your prompt to avoid potential policy violations
    • Describing the scene rather than uploading an image

    “Copyright Violation” Errors

    If you receive this message, rephrase your prompt to avoid direct mention of copyrighted properties13. For example:

    • Instead of “Studio Ghibli style,” try “dreamy Japanese animation style”
    • Instead of mentioning specific Ghibli films, describe the visual style you want

    Ethical Considerations

    While creating Ghibli-style images is fun, it’s worth noting that Miyazaki himself has expressed skepticism about AI’s role in animation12. When sharing your AI-generated artwork:

    • Acknowledge they are AI-generated
    • Use them for personal enjoyment rather than commercial purposes
    • Be mindful of the ongoing discussions about AI and creative works

    Final Thoughts

    The Ghibli style image trend showcases how AI is making artistic styles more accessible to everyone. While ChatGPT Plus offers polished results, the free alternatives outlined here provide excellent options for joining this creative movement without spending money.

    Whether you choose Gemini AI, Grok, or other free image generators, you can now transform your photos into magical Ghibli-inspired artwork that captures that special blend of wonder and nostalgia. Try these methods today and share your creations with friends – you might be surprised by how magical your ordinary photos can become!

    Building Your Own Quadcopter Drone: Essential Parts and Specifications in India

    Shounak Das
    -
    0

    Drones have captured the imagination of hobbyists, engineers, and professionals alike. Building your own quadcopter drone can be an exciting and rewarding experience. Here, we’ll outline the essential components, their specifications, and tips to assemble your very own quadcopter. Links to purchase components are included to make your journey seamless.

    Essential Components to Build a Quadcopter

    1. Brushless Motors (e.g., A2212 1000KV)

    • Purpose: Provide lift and thrust to keep the drone airborne.
    • Specification: A2212 1000KV motors are popular for their efficiency and compatibility with most quadcopter setups.
    • Quantity: 4 (one for each arm of the quadcopter).
    • Where to Buy: A2212 1000KV Brushless Motor.
    Buy

    2. Electronic Speed Controllers (ESC) (e.g., SimonK 30A)

    • Purpose: Regulate power from the battery to the motors.
    • Specification: 30A ESCs are ideal for smooth motor control and support for 2-3S LiPo batteries.
    • Quantity: 4 (one for each motor).
    • Where to Buy: SimonK 30A ESC.
    Buy

    3. Flight Control Board (e.g., ARDUCOPTER APM 2.8)

    • Purpose: Acts as the brain of the drone, handling flight stabilization and controls.
    • Specification: The APM 2.8 is beginner-friendly and supports GPS and additional sensors.
    • Where to Buy: ARDUCOPTER APM 2.8.
    Buy

    4. LiPo Battery (e.g., 11.1V 2200mAh)

    • Purpose: Powers the motors and electronics.
    • Specification: 11.1V 2200mAh is a common choice for drones due to its balance of capacity and weight.
    • Where to Buy: 11.1V 2200mAh LiPo Battery.
    Buy

    5. Quadcopter Frame (e.g., F450 / Q450 Frame)

    • Purpose: Provides structure and houses all components.
    • Specification: Integrated PCB version simplifies wiring and ensures durability.
    • Where to Buy: F450 / Q450 Frame.
    Buy

    6. Propellers (e.g., 10×4.5 ABS Propellers)

    • Purpose: Generate thrust to lift the drone.
    • Specification: ABS propellers are lightweight and durable; use pairs of clockwise (CW) and counterclockwise (CCW).
    • Quantity: 2 pairs
    • Where to Buy: Orange HD Propellers.
    Buy

    7. Power Distribution Module (e.g., APM/Pixhawk Power Module V6.0)

    • Purpose: Supplies power to the flight controller and motors.
    • Specification: Capable of handling 28V and 90A, with a built-in BEC.
    • Where to Buy: Pixhawk Power Module.
    Buy

    8. Charger (e.g., IMax B3)

    • Purpose: Safely recharges your LiPo battery.
    • Specification: Compact and compatible with 2-3S batteries.
    • Where to Buy: IMax B3 Charger.
    Buy

    9. Others

    Specifications of the Quadcopter

    • Weight: ~1.2-1.5 kg (depending on additional accessories).
    • Flight Time: 8-12 minutes (with a 2200mAh LiPo battery).
    • Range: ~300-5000 meters (dependent on transmitter and receiver).
    • Thrust-to-Weight Ratio: >2:1 (ensures stable flight).

    Assembly Tips

    1. Frame Setup: Assemble the F450 frame and secure motors to each arm.
    2. Wiring the ESCs: Connect the ESCs to the motors and the integrated PCB on the frame.
    3. Flight Controller: Mount the APM 2.8 board at the center for optimal stability.
    4. Power Distribution: Use the Pixhawk Power Module to connect the battery and provide power to all components.
    5. Propeller Installation: Attach CW and CCW propellers to the correct motors.
    6. Battery Placement: Secure the LiPo battery at the bottom or center for balance.

    Why Build Your Own Drone?

    • Customization: Tailor specifications to your needs.
    • Learning Experience: Understand aerodynamics, electronics, and software integration.
    • Cost Efficiency: Often cheaper than buying a ready-made drone.

    Building your drone is not only fulfilling but also a gateway to understanding robotics and IoT. Start your journey today by gathering these components and bringing your quadcopter to life!

    Airdrops You Should Join Like I Did in 2025 | Part 2

    Shounak Das
    -
    0
    Airdrops You Should Join Like I Did in 2025 | Part 2

    As someone who actively participates in crypto airdrops, I’ve uncovered some of the most promising opportunities this year. Airdrops are not just about free tokens; they’re a gateway to exploring new blockchain projects and technologies. In this post, I’ll share the next set of airdrops you shouldn’t miss in 2024. These projects are making waves in the crypto space, and by joining them, you can earn rewards while supporting innovation.

    1. DeNet: Decentralized Web Services

    DeNet is redefining web hosting and data storage with its decentralized, secure, and cost-effective platform. By eliminating reliance on centralized cloud providers, DeNet empowers users to host websites and store files securely. Participants in the DeNet airdrop can receive free DNET tokens by joining their community on Discord, following their social media channels, and completing simple tasks.

    DeNet
    • How to Participate: Sign up on the official DeNet website, complete tasks, and claim your free tokens.
    • Why It’s Exciting: DeNet’s decentralized approach challenges traditional cloud giants, giving users control and reducing costs. Early adopters can benefit from being part of this transformative project.

    2. AlphaOS: Blockchain Operating System

    AlphaOS aims to create an operating system optimized for blockchain applications. This innovative platform offers enhanced security, seamless blockchain integration, and a developer-friendly environment. Early adopters who join the AlphaOS airdrop can secure exclusive rewards and early access to their ecosystem.

    AlphaOS
    • How to Participate: Register on the AlphaOS platform and engage in promotional activities.
    • Why It’s Exciting: As blockchain adoption grows, AlphaOS is positioning itself as the backbone for decentralized applications. Their airdrop rewards can provide a valuable stake in this emerging ecosystem.

    3. Kaiser ZeroNode: Decentralized VPN Solution

    Kaiser ZeroNode is revolutionizing online privacy with its decentralized VPN, offering users anonymity and data protection without relying on centralized servers. This project’s unique approach ensures that users retain control over their internet connections. Joining their airdrop program provides free tokens and early access to their beta platform.

    Kaiser ZeroNode
    • How to Participate: Follow Kaiser ZeroNode’s official social media accounts and join their Telegram group to complete tasks and earn tokens.
    • Why It’s Exciting: Privacy is a growing concern, and Kaiser ZeroNode’s decentralized VPN is a game-changer for secure and anonymous browsing.

    4. Bless: Blockchain-based Donation Platform

    Bless leverages blockchain technology to create a transparent and efficient donation platform. By connecting donors directly with recipients, it ensures that every contribution is accounted for and maximized. Bless’s airdrop rewards participants with tokens for signing up, promoting the platform, and engaging in its community.

    Bless
    • How to Participate: Visit the Bless website, register, and share their mission on social media to claim your tokens.
    • Why It’s Exciting: Bless’s mission to make donations transparent and impactful resonates with the values of blockchain technology. Being part of this initiative is both rewarding and meaningful.

    5. OpenLoop: Decentralized Freelance Marketplace

    OpenLoop aims to disrupt the freelancing industry by creating a decentralized platform where freelancers and clients can connect without hefty commissions. With built-in smart contracts ensuring fair payments and dispute resolution, OpenLoop is set to become a game-changer. Their airdrop offers free tokens for completing onboarding tasks.

    OpenLoop
    • How to Participate: Sign up on the OpenLoop platform, complete your profile, and refer friends to earn tokens.
    • Why It’s Exciting: Freelancers and clients can benefit from lower costs and greater transparency. OpenLoop’s vision aligns perfectly with the decentralized ethos.

    Why Airdrops Matter to Me

    Participating in airdrops has allowed me to discover and support emerging projects while earning tokens that often appreciate in value. It’s also a way to stay ahead in the fast-evolving crypto space. By engaging with these projects, I’ve not only gained financial rewards but also insights into groundbreaking technologies.

    Tips to Maximize Airdrop Opportunities

    1. Stay Informed: Follow official project channels on social media to get timely updates.
    2. Use Secure Wallets: Ensure you’re using wallets compatible with the project’s blockchain.
    3. Engage Actively: Many projects reward community engagement, so participate in discussions and activities.
    4. Verify Information: Only follow official links to avoid scams.

    Final Thoughts

    These airdrops offer more than just free tokens; they provide a chance to be part of revolutionary projects shaping the future of blockchain technology. By joining these airdrops, you can diversify your crypto portfolio while supporting innovation. Don’t miss out—take the plunge and explore these opportunities today!

    123...8Page 1 of 8
    - Advertisement -

    Contact us: contact@thescience360.com

    FOLLOW US