A practical and comprehensive look at the tiny AVR microcontroller family
The ATtiny25 ATtiny45 and ATtiny85 are widely used in embedded electronics because they offer a strong balance of performance, size and power efficiency. These microcontrollers are ideal for compact devices including wearables, sensor modules, lighting controllers, robotics and low-power automation systems.
This guide covers everything from pinout and memory to peripherals programming methods and practical design tips. It is written to be fast to read and highly informative for both beginners and professionals.
1. Why the ATtiny25 ATtiny45 ATtiny85 Remain So Popular
According to the official Atmel datasheet, these devices use an 8-bit AVR RISC architecture capable of nearly one instruction per clock cycle. This allows efficient execution of control loops timing routines sensor sampling and communication tasks. The internal oscillator, low-power modes and compact 8-pin package make them ideal for battery-driven and space-limited designs.
Key strengths
- Works from 1.8 V to 5.5 V
- Runs up to 20 MHz at higher voltages
- Integrated 8 MHz calibrated RC oscillator
- Six multipurpose GPIO pins
- SPI and I2C compatible communication using USI
- 10-bit ADC with multiple channels
- Low power consumption down to microamp levels during sleep
- Available in PDIP, SOIC and QFN packages
Memory options
The three variants differ mainly by their memory size.
| Device | Flash | SRAM | EEPROM |
|---|---|---|---|
| ATtiny25 | 2 KB | 128 B | 128 B |
| ATtiny45 | 4 KB | 256 B | 256 B |
| ATtiny85 | 8 KB | 512 B | 512 B |
Most makers choose the ATtiny85 for projects requiring libraries or complex logic, while the ATtiny25 is excellent for simple controllers or repetitive logic tasks.
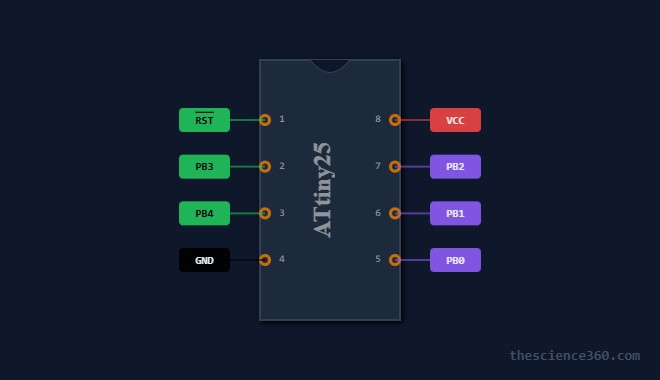
2. ATtiny25 ATtiny45 ATtiny85 Pinout Explained
The devices share the same 8-pin pinout, making it easy to upgrade or downgrade based on memory needs. The pinout diagram on page 2 of the datasheet shows the mapping clearly.
Pin functions
| Pin | Label | Primary Roles |
|---|---|---|
| 1 | PB5 | Reset, ADC0, PCINT5, debugWIRE |
| 2 | PB3 | XTAL1, CLKI, ADC3, OC1B |
| 3 | PB4 | XTAL2, CLKO, ADC2 |
| 4 | GND | Ground |
| 5 | PB0 | MOSI, SDA, AIN0, OC0A, AREF |
| 6 | PB1 | MISO, AIN1, OC0B, OC1A |
| 7 | PB2 | SCK, SCL, ADC1, INT0, Timer0 |
| 8 | VCC | Power |
Each pin supports several alternate functions, so planning pin usage carefully is important for larger projects.
3. Internal Architecture and Processing Capability
The ATtiny series uses a compact AVR RISC architecture with 32 working registers that connect directly to the arithmetic logic unit. This eliminates unnecessary memory access cycles and significantly improves execution speed. The datasheet notes that the microcontroller can achieve one MIPS per MHz, improving power and timing efficiency compared to older classic microcontrollers.
What this means for real applications
- Smooth control loops for robotics
- Stable timers for PWM generation
- Reliable sampling for sensors
- Consistent timing without jitter
4. Memory System Overview
Flash memory
Used for program storage.
Reprogrammable up to ten thousand times.
EEPROM
For storing configuration values, calibration data or logs.
SRAM
Stores variables stack data and buffers.
Since the ATtiny85 has the most memory, it is recommended for applications using communication libraries or handling real-time data.
5. Peripherals That Expand What the ATtiny Can Do
Despite its small package the ATtiny25 ATtiny45 ATtiny85 include a surprisingly rich set of peripherals.
5.1 Timers and PWM capability
- Timer Counter 0: 8-bit with two PWM outputs
- Timer Counter 1: High-speed 8-bit timer with dead-time generator and separate prescaler
These timers make the ATtiny family suitable for:
- LED brightness control
- Motor speed control
- Generating precise waveforms
- Driving servos
5.2 10-bit ADC
Includes four single-ended channels and two differential channels with programmable gain. The ADC can measure voltages sensors and even temperature thanks to an internal temperature sensor referenced in the datasheet.
Ideal for:
- Motion sensors
- Temperature loggers
- Battery measurement
- Analog controllers
5.3 USI (Universal Serial Interface)
The USI can act as:
- SPI master or slave
- Two-wire I2C-like interface
- General synchronous serial interface
Although not a full I2C hardware unit, it is flexible enough for communicating with most sensors or memory chips.
5.4 Watchdog timer
Has its own oscillator allowing the microcontroller to recover automatically from program hangs or unexpected faults.
5.5 Analog comparator
Useful for:
- Zero-cross detection
- Battery threshold checks
- Overcurrent detection
6. Clock Sources and Performance Scaling
The ATtiny series supports multiple clock sources, including the internal RC oscillator, external crystal and external clock input. A PLL option exists in some revisions for generating a fast peripheral clock, as seen in the datasheet block diagrams.
Designers can fine-tune performance and energy use using the clock prescaler. Lower clock speeds reduce power consumption while still allowing timing-driven tasks to run accurately.
7. Power Management and Sleep Modes
Power efficiency is one of the main reasons these devices continue to be used widely. The ATtiny25 ATtiny45 ATtiny85 include several power-saving modes.
Available sleep modes
- Idle mode
- ADC Noise Reduction mode
- Power down mode
Power down mode brings consumption as low as 0.1 microamp at 1.8 V according to the datasheet. This is ideal for IoT sensors and wearable devices.
Techniques to reduce power
- Turn off unused peripherals via the Power Reduction Register
- Disable the ADC when not actively measuring
- Rely on watchdog interrupts for periodic wakeups
- Use pin change interrupts for responding to events
8. Programming Methods
8.1 ISP (In-System Programming)
The most common method is through SPI using:
- PB0 (MOSI)
- PB1 (MISO)
- PB2 (SCK)
- PB5 (RESET)
Popular programmers:
- USBasp
- AVRISP mkII
- Arduino used as ISP
8.2 Arduino IDE support
You can program the ATtiny family using the Arduino IDE by installing a proper core such as ATTinyCore.
Steps:
- Install the core
- Select the ATtiny variant
- Choose the clock (often internal 8 MHz)
- Burn bootloader to set fuses
- Upload program through programmer
8.3 debugWIRE
PB5 doubles as the debugWIRE interface which can be used for on-chip debugging. The datasheet lists debugWIRE under its special features.
9. Example Applications
9.1 Compact temperature logger
Uses: ADC, internal temperature sensor, EEPROM storage and watchdog for timed wakeups.
9.2 Wearable sensor modules
Uses: USI for I2C accelerometer, PWM for feedback and low-power sleep cycles.
9.3 Mini robotics controller
Uses: PWM for motor control, ADC for sensors, interrupts for quick response.
9.4 LED lighting systems
Uses: Timer0 and Timer1 PWM channels for precise brightness control.
10. Choosing Between ATtiny25 ATtiny45 ATtiny85
| Application Type | Suggested Variant |
|---|---|
| Simple timing or logic | ATtiny25 |
| Sensor reading and basic control loops | ATtiny45 |
| Projects requiring libraries or communication stacks | ATtiny85 |
The ATtiny85 is the most versatile and frequently used option.
11. Engineering Tips for Better Performance
11.1 Plan pin usage carefully
Since the chip has only six GPIO pins, map peripherals early in your design to avoid conflicts.
11.2 Use power reduction options
Disable unused modules like USI, ADC or timers to extend battery life.
11.3 Manage the reset pin with caution
PB5 can be turned into a GPIO only by disabling the reset fuse, but this requires high-voltage programming to recover. Use this only when absolutely necessary.
11.4 Avoid EEPROM reads at very low clock speeds
The datasheet warns that reading EEPROM below about 900 kHz internal clock may fail on certain device revisions.
12. Known Limitations and Errata Insights
The datasheet lists several errata items:
- EEPROM read issues below 900 kHz on some revisions
- PLL lock issues below 6 MHz on older ATtiny45 revisions
- Some PWM output behavior differences in older silicon versions
Checking the revision code on your chip and verifying it with the errata section ensures stable operation.
13. Final Thoughts
The ATtiny25 ATtiny45 and ATtiny85 deliver a remarkable mix of capability and efficiency in a very small footprint. Their strong peripheral set, reliable timing features and low power consumption make them suitable for a wide range of modern embedded applications. Whether you are building wearables, compact robots, smart lighting or low-power sensors, the ATtiny family provides exactly the right balance of performance, flexibility and simplicity.




 400 a night.” Comet will then scour the web, compare options, and present you with a personalized itinerary.
400 a night.” Comet will then scour the web, compare options, and present you with a personalized itinerary.
![Rendered by QuickLaTeX.com 146 this month</strong> by leveraging legit beer money sites and testing platforms. <!-- /wp:paragraph --> <!-- wp:paragraph --> Let's dive in. <!-- /wp:paragraph --> <!-- wp:paragraph {"dropCapStyle":"dropcapp"} --> Summary Table: <!-- /wp:paragraph --> <!-- wp:html --> <style type="text/css">@import url("https://assets.mlcdn.com/fonts.css?version=1750852");</style> <style type="text/css"> /* LOADER */ .ml-form-embedSubmitLoad { display: inline-block; width: 20px; height: 20px; } .g-recaptcha { transform: scale(1); -webkit-transform: scale(1); transform-origin: 0 0; -webkit-transform-origin: 0 0; height: ; } .sr-only { position: absolute; width: 1px; height: 1px; padding: 0; margin: -1px; overflow: hidden; clip: rect(0,0,0,0); border: 0; } .ml-form-embedSubmitLoad:after { content: " "; display: block; width: 11px; height: 11px; margin: 1px; border-radius: 50%; border: 4px solid #fff; border-color: #ffffff #ffffff #ffffff transparent; animation: ml-form-embedSubmitLoad 1.2s linear infinite; } @keyframes ml-form-embedSubmitLoad { 0% { transform: rotate(0deg); } 100% { transform: rotate(360deg); } } #mlb2-27858390.ml-form-embedContainer { box-sizing: border-box; display: table; margin: 0 auto; position: static; width: 100% !important; } #mlb2-27858390.ml-form-embedContainer h4, #mlb2-27858390.ml-form-embedContainer p, #mlb2-27858390.ml-form-embedContainer span, #mlb2-27858390.ml-form-embedContainer button { text-transform: none !important; letter-spacing: normal !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper { background-color: #f6f6f6; border-width: 0px; border-color: transparent; border-radius: 4px; border-style: solid; box-sizing: border-box; display: inline-block !important; margin: 0; padding: 0; position: relative; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper.embedPopup, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper.embedDefault { width: 400px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper.embedForm { max-width: 400px; width: 100%; } #mlb2-27858390.ml-form-embedContainer .ml-form-align-left { text-align: left; } #mlb2-27858390.ml-form-embedContainer .ml-form-align-center { text-align: center; } #mlb2-27858390.ml-form-embedContainer .ml-form-align-default { display: table-cell !important; vertical-align: middle !important; text-align: center !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-align-right { text-align: right; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedHeader img { border-top-left-radius: 4px; border-top-right-radius: 4px; height: auto; margin: 0 auto !important; max-width: 100%; width: undefinedpx; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody { padding: 20px 20px 0 20px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody.ml-form-embedBodyHorizontal { padding-bottom: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent { text-align: left; margin: 0 0 20px 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent h4, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent h4 { color: #000000; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 30px; font-weight: 400; margin: 0 0 10px 0; text-align: left; word-break: break-word; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent p, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent p { color: #000000; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px; font-weight: 400; line-height: 20px; margin: 0 0 10px 0; text-align: left; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent ul, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent ol, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent ul, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent ol { color: #000000; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent ol ol, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent ol ol { list-style-type: lower-alpha; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent ol ol ol, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent ol ol ol { list-style-type: lower-roman; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent p a, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent p a { color: #000000; text-decoration: underline; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-block-form .ml-field-group { text-align: left!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-block-form .ml-field-group label { margin-bottom: 5px; color: #333333; font-size: 14px; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-weight: bold; font-style: normal; text-decoration: none;; display: inline-block; line-height: 20px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedContent p:last-child, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-successBody .ml-form-successContent p:last-child { margin: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody form { margin: 0; width: 100%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-formContent, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow { margin: 0 0 20px 0; width: 100%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow { float: left; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-formContent.horozintalForm { margin: 0; padding: 0 0 20px 0; width: 100%; height: auto; float: left; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow { margin: 0 0 10px 0; width: 100%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow.ml-last-item { margin: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow.ml-formfieldHorizintal { margin: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input { background-color: #ffffff !important; color: #333333 !important; border-color: #cccccc; border-radius: 4px !important; border-style: solid !important; border-width: 1px !important; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px !important; height: auto; line-height: 21px !important; margin-bottom: 0; margin-top: 0; margin-left: 0; margin-right: 0; padding: 10px 10px !important; width: 100% !important; box-sizing: border-box !important; max-width: 100% !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input::-webkit-input-placeholder, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow input::-webkit-input-placeholder { color: #333333; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input::-moz-placeholder, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow input::-moz-placeholder { color: #333333; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input:-ms-input-placeholder, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow input:-ms-input-placeholder { color: #333333; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input:-moz-placeholder, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow input:-moz-placeholder { color: #333333; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow textarea, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow textarea { background-color: #ffffff !important; color: #333333 !important; border-color: #cccccc; border-radius: 4px !important; border-style: solid !important; border-width: 1px !important; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px !important; height: auto; line-height: 21px !important; margin-bottom: 0; margin-top: 0; padding: 10px 10px !important; width: 100% !important; box-sizing: border-box !important; max-width: 100% !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::before { border-color: #cccccc!important; background-color: #ffffff!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow input.custom-control-input[type="checkbox"]{ box-sizing: border-box; padding: 0; position: absolute; z-index: -1; opacity: 0; margin-top: 5px; margin-left: -1.5rem; overflow: visible; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::before { border-radius: 4px!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow input[type=checkbox]:checked~.label-description::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox input[type=checkbox]:checked~.label-description::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-input:checked~.custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-input:checked~.custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox input[type=checkbox]:checked~.label-description::after { background-image: url("data:image/svg+xml,%3csvg xmlns='http://www.w3.org/2000/svg' viewBox='0 0 8 8'%3e%3cpath fill='%23fff' d='M6.564.75l-3.59 3.612-1.538-1.55L0 4.26 2.974 7.25 8 2.193z'/%3e%3c/svg%3e"); } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-input:checked~.custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-input:checked~.custom-control-label::after { background-image: url("data:image/svg+xml,%3csvg xmlns='http://www.w3.org/2000/svg' viewBox='-4 -4 8 8'%3e%3ccircle r='3' fill='%23fff'/%3e%3c/svg%3e"); } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-input:checked~.custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-input:checked~.custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-input:checked~.custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-input:checked~.custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox input[type=checkbox]:checked~.label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox input[type=checkbox]:checked~.label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow input[type=checkbox]:checked~.label-description::before { border-color: #000000!important; background-color: #000000!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-label::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-label::after { top: 2px; box-sizing: border-box; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::after { top: 0px!important; box-sizing: border-box!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::after { top: 0px!important; box-sizing: border-box!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::after { top: 0px!important; box-sizing: border-box!important; position: absolute; left: -1.5rem; display: block; width: 1rem; height: 1rem; content: ""; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::before { top: 0px!important; box-sizing: border-box!important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .custom-control-label::before { position: absolute; top: 4px; left: -1.5rem; display: block; width: 16px; height: 16px; pointer-events: none; content: ""; background-color: #ffffff; border: #adb5bd solid 1px; border-radius: 50%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .custom-control-label::after { position: absolute; top: 2px!important; left: -1.5rem; display: block; width: 1rem; height: 1rem; content: ""; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::before, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::before { position: absolute; top: 4px; left: -1.5rem; display: block; width: 16px; height: 16px; pointer-events: none; content: ""; background-color: #ffffff; border: #adb5bd solid 1px; border-radius: 50%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::after { position: absolute; top: 0px!important; left: -1.5rem; display: block; width: 1rem; height: 1rem; content: ""; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::after { position: absolute; top: 0px!important; left: -1.5rem; display: block; width: 1rem; height: 1rem; content: ""; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .custom-radio .custom-control-label::after { background: no-repeat 50%/50% 50%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .custom-checkbox .custom-control-label::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedPermissions .ml-form-embedPermissionsOptionsCheckbox .label-description::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-interestGroupsRow .ml-form-interestGroupsRowCheckbox .label-description::after, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description::after { background: no-repeat 50%/50% 50%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-control, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-control { position: relative; display: block; min-height: 1.5rem; padding-left: 1.5rem; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-input, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-input, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-input, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-input { position: absolute; z-index: -1; opacity: 0; box-sizing: border-box; padding: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-radio .custom-control-label, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-radio .custom-control-label, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-checkbox .custom-control-label, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-checkbox .custom-control-label { color: #000000; font-size: 12px!important; font-family: 'Open Sans', Arial, Helvetica, sans-serif; line-height: 22px; margin-bottom: 0; position: relative; vertical-align: top; font-style: normal; font-weight: 700; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-fieldRow .custom-select, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow .custom-select { background-color: #ffffff !important; color: #333333 !important; border-color: #cccccc; border-radius: 4px !important; border-style: solid !important; border-width: 1px !important; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px !important; line-height: 20px !important; margin-bottom: 0; margin-top: 0; padding: 10px 28px 10px 12px !important; width: 100% !important; box-sizing: border-box !important; max-width: 100% !important; height: auto; display: inline-block; vertical-align: middle; background: url('https://assets.mlcdn.com/ml/images/default/dropdown.svg') no-repeat right .75rem center/8px 10px; -webkit-appearance: none; -moz-appearance: none; appearance: none; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow { height: auto; width: 100%; float: left; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .ml-input-horizontal { width: 70%; float: left; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .ml-button-horizontal { width: 30%; float: left; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .ml-button-horizontal.labelsOn { padding-top: 25px; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .horizontal-fields { box-sizing: border-box; float: left; padding-right: 10px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow input { background-color: #ffffff; color: #333333; border-color: #cccccc; border-radius: 4px; border-style: solid; border-width: 1px; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px; line-height: 20px; margin-bottom: 0; margin-top: 0; padding: 10px 10px; width: 100%; box-sizing: border-box; overflow-y: initial; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow button { background-color: #004169 !important; border-color: #004169; border-style: solid; border-width: 1px; border-radius: 4px; box-shadow: none; color: #ffffff !important; cursor: pointer; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 14px !important; font-weight: 700; line-height: 20px; margin: 0 !important; padding: 10px !important; width: 100%; height: auto; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-horizontalRow button:hover { background-color: #333333 !important; border-color: #333333 !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow input[type="checkbox"] { box-sizing: border-box; padding: 0; position: absolute; z-index: -1; opacity: 0; margin-top: 5px; margin-left: -1.5rem; overflow: visible; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow .label-description { color: #000000; display: block; font-family: 'Open Sans', Arial, Helvetica, sans-serif; font-size: 12px; text-align: left; margin-bottom: 0; position: relative; vertical-align: top; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow label { font-weight: normal; margin: 0; padding: 0; position: relative; display: block; min-height: 24px; padding-left: 24px; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow label a { color: #000000; text-decoration: underline; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow label p { color: #000000 !important; font-family: 'Open Sans', Arial, Helvetica, sans-serif !important; font-size: 12px !important; font-weight: normal !important; line-height: 18px !important; padding: 0 !important; margin: 0 5px 0 0 !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow label p:last-child { margin: 0; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedSubmit { margin: 0 0 20px 0; float: left; width: 100%; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedSubmit button { background-color: #004169 !important; border: none !important; border-radius: 4px !important; box-shadow: none !important; color: #ffffff !important; cursor: pointer; font-family: 'Open Sans', Arial, Helvetica, sans-serif !important; font-size: 14px !important; font-weight: 700 !important; line-height: 21px !important; height: auto; padding: 10px !important; width: 100% !important; box-sizing: border-box !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedSubmit button.loading { display: none; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-embedSubmit button:hover { background-color: #333333 !important; } .ml-subscribe-close { width: 30px; height: 30px; background: url('https://assets.mlcdn.com/ml/images/default/modal_close.png') no-repeat; background-size: 30px; cursor: pointer; margin-top: -10px; margin-right: -10px; position: absolute; top: 0; right: 0; } .ml-error input, .ml-error textarea, .ml-error select { border-color: red!important; } .ml-error .custom-checkbox-radio-list { border: 1px solid red !important; border-radius: 4px; padding: 10px; } .ml-error .label-description, .ml-error .label-description p, .ml-error .label-description p a, .ml-error label:first-child { color: #ff0000 !important; } #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow.ml-error .label-description p, #mlb2-27858390.ml-form-embedContainer .ml-form-embedWrapper .ml-form-embedBody .ml-form-checkboxRow.ml-error .label-description p:first-letter { color: #ff0000 !important; } @media only screen and (max-width: 400px){ .ml-form-embedWrapper.embedDefault, .ml-form-embedWrapper.embedPopup { width: 100%!important; } .ml-form-formContent.horozintalForm { float: left!important; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow { height: auto!important; width: 100%!important; float: left!important; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .ml-input-horizontal { width: 100%!important; } .ml-form-formContent.horozintalForm .ml-form-horizontalRow .ml-input-horizontal > div { padding-right: 0px!important; padding-bottom: 10px; } .ml-form-formContent.horozintalForm .ml-button-horizontal { width: 100%!important; } .ml-form-formContent.horozintalForm .ml-button-horizontal.labelsOn { padding-top: 0px!important; } } </style> <div id="mlb2-27858390" class="ml-form-embedContainer ml-subscribe-form ml-subscribe-form-27858390"> <div class="ml-form-align-center "> <div class="ml-form-embedWrapper embedForm"> <div class="ml-form-embedBody ml-form-embedBodyDefault row-form"> <div class="ml-form-embedContent" style=" "> <h4>My report</h4> Beer Money Report: Monthly Report and sites </div> <form class="ml-block-form" action="https://assets.mailerlite.com/jsonp/999177/forms/158706521894553421/subscribe" data-code="" method="post" target="_blank"> <div class="ml-form-formContent"> <div class="ml-form-fieldRow ml-last-item"> <div class="ml-field-group ml-field-email ml-validate-email ml-validate-required"> <!-- input --> <input aria-label="email" aria-required="true" type="email" class="form-control" data-inputmask="" name="fields[email]" placeholder="Email" autocomplete="email"> <!-- /input --> <!-- textarea --> <!-- /textarea --> <!-- select --> <!-- /select --> <!-- checkboxes --> <!-- /checkboxes --> <!-- radio --> <!-- /radio --> <!-- countries --> <!-- /countries --> </div> </div> </div> <!-- Privacy policy --> <!-- /Privacy policy --> <input type="hidden" name="ml-submit" value="1"> <div class="ml-form-embedSubmit"> <button type="submit" class="primary">Subscribe</button> <button disabled="disabled" style="display: none;" type="button" class="loading"> <div class="ml-form-embedSubmitLoad"></div> <span class="sr-only">Loading...</span> </button> </div> <input type="hidden" name="anticsrf" value="true"> </form> </div> <div class="ml-form-successBody row-success" style="display: none"> <div class="ml-form-successContent"> <h4>Thank you!</h4> You have successfully joined the Best Beer Money List </div> </div> </div> </div> </div> <script> function ml_webform_success_27858390() { var](https://thescience360.com/wp-content/ql-cache/quicklatex.com-2772166d6ea304283e93c32b8f346427_l3.png) = ml_jQuery || jQuery;
= ml_jQuery || jQuery;
 5
5 10
10 25
25 10
10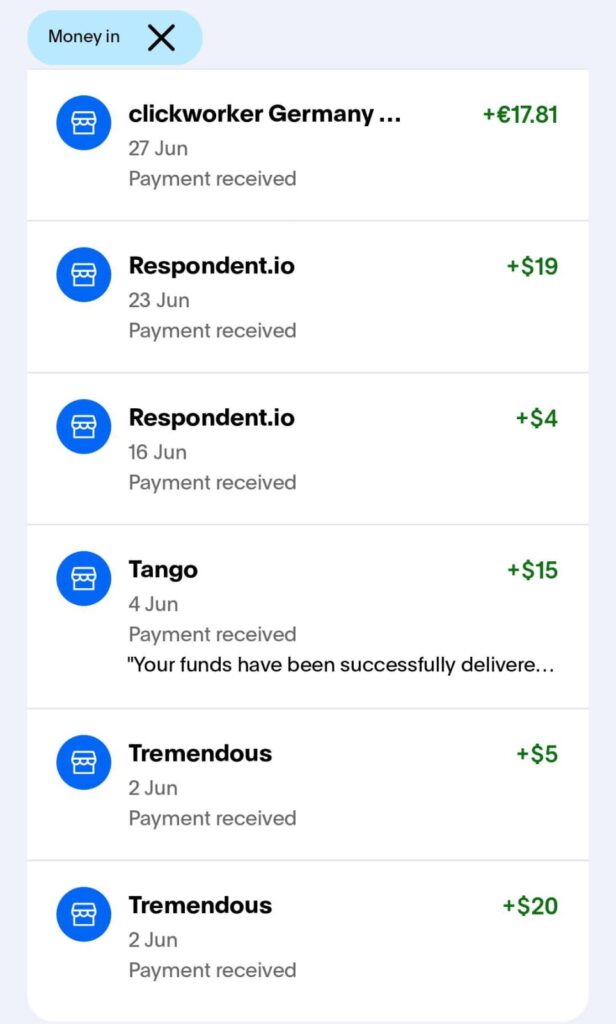
 21
21 5
5 15
15 10 (after several weeks of accumulating points)
10 (after several weeks of accumulating points) 40
40 10
10 5
5